网址:http://m.1010jiajiao.com/timu_id_480934[举报]
一个等比数列的首项为1,项数是偶数,其奇数项的和为85,偶数项的和为170,求此数列的公比和项数.
思路分析:因奇数项和与偶数项和不同,项数相同,可知其公比q≠1,故可直接套用求和公式,列方程组解决.
查看习题详情和答案>>已知 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
.
(Ⅰ)求数列 与
与 的通项公式;
的通项公式;
(Ⅱ)记 ,
, ,证明
,证明 (
( ).
).
【解析】(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得
所以 ,
, ,
, .
.
(2)证明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:数学归纳法)
① 当n=1时,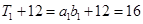 ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即 ,则当n=k+1时,有:
,则当n=k+1时,有:






即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意 ,
, 成立.
成立.
查看习题详情和答案>>
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,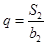 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足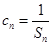 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
【解析】本试题主要是考查了等比数列的通项公式和求和的运用。第一问中,利用等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,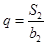 ,可得
,可得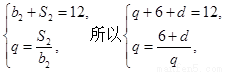 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,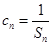 ,由第一问中知道
,由第一问中知道 ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.
解: (Ⅰ) 设:{an}的公差为d,
因为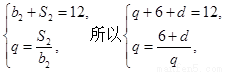 解得q=3或q=-4(舍),d=3.
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n, bn=3 n-1. ………6分
(Ⅱ)因为 ……………8分
……………8分
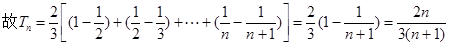
查看习题详情和答案>>
已知等差数列{an}的首项为4,公差为4,其前n项和为Sn,则数列 {![]() }的前n项和为( )
}的前n项和为( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考点: | 数列的求和;等差数列的性质. |
| 专题: | 等差数列与等比数列. |
| 分析: | 利用等差数列的前n项和即可得出Sn,再利用“裂项求和”即可得出数列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴数列 { 故选A. |
| 点评: | 熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键. |
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
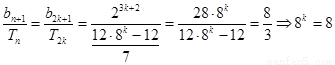
 ,
,
查看习题详情和答案>>