摘要:(Ⅱ)设.则(显然)
网址:http://m.1010jiajiao.com/timu_id_480917[举报]
已知 中,
中, ,
, .设
.设 ,记
,记 .
.
(1) 求 的解析式及定义域;
的解析式及定义域;
(2)设 ,是否存在实数
,是否存在实数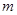 ,使函数
,使函数 的值域为
的值域为 ?若存在,求出
?若存在,求出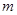 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问利用(1)如图,在 中,由
中,由 ,,
,,
可得 ,
,
又AC=2,故由正弦定理得

(2)中
由 可得
可得

 .显然,
.显然, ,则
,则
1 当m>0的值域为
当m>0的值域为
 m+1=3/2,n=1/2
m+1=3/2,n=1/2
2 当m<0,不满足
当m<0,不满足 的值域为
的值域为 ;
;
因而存在实数m=1/2 的值域为
的值域为 .
.
查看习题详情和答案>>
考察等式:
 (*)
(*)
其中n,m,r∈N*,r≤m<n且r≤n-m,
某同学用概率论方法证明等式(*)如下:设一批产品共有n件,其中m件是次品,其余为正品,现从中随机取出r件产品,记事件Ak={取到的r件产品中恰有k件次品},则 ,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且
,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
,
所以, ,即等式(*)成立。
,即等式(*)成立。
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.
现有以下四个判断:①等式(*)成立;②等式(*)不成立;③证明正确;④证明不正确,试写出所有正确判断的序号( )。
查看习题详情和答案>>
 (*)
(*)其中n,m,r∈N*,r≤m<n且r≤n-m,
某同学用概率论方法证明等式(*)如下:设一批产品共有n件,其中m件是次品,其余为正品,现从中随机取出r件产品,记事件Ak={取到的r件产品中恰有k件次品},则
 ,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且
,k=0,1,…,r。显然A0,A1,…,Ar为互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
,所以,
 ,即等式(*)成立。
,即等式(*)成立。对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.
现有以下四个判断:①等式(*)成立;②等式(*)不成立;③证明正确;④证明不正确,试写出所有正确判断的序号( )。
(2009•金山区二模)设函数f(x)=x2+x.(1)解不等式:f(x)<0;(2)请先阅读下列材料,然后回答问题.
材料:已知函数g(x)=-
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
解:令u=-f(x)=-x2-x,则u=-(x+
)2+
,
当x=-
时,u有最大值,umax=
,显然u没有最小值,
∴当x=-
时,g(x)有最小值4,没有最大值.
请回答:上述解答是否正确?若不正确,请给出正确的解答;
(3)设an=
,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
注意:第(3)题中所提问题单独给分,.解答也单独给分.本题按照所提问题的难度分层给分,解答也相应给分,如果同时提出两个问题,则就高不就低,解答也相同处理.
查看习题详情和答案>>
材料:已知函数g(x)=-
| 1 |
| f(x) |
解:令u=-f(x)=-x2-x,则u=-(x+
| 1 |
| 2 |
| 1 |
| 4 |
当x=-
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=-
| 1 |
| 2 |
请回答:上述解答是否正确?若不正确,请给出正确的解答;
(3)设an=
| f(n) |
| 2n-1 |
注意:第(3)题中所提问题单独给分,.解答也单独给分.本题按照所提问题的难度分层给分,解答也相应给分,如果同时提出两个问题,则就高不就低,解答也相同处理.
考察等式:
+
+…+
=
(*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同学用概率论方法证明等式(*)如下:
设一批产品共有n件,其中m件是次品,其余为正品.现从中随机取出r件产品,
记事件Ak={取到的r件产品中恰有k件次品},则P(Ak)=
,k=0,1,2,…,r.
显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,
所以
+
+…+
=
,即等式(*)成立.
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
①等式(*)成立 ②等式(*)不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号______.
查看习题详情和答案>>
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
设一批产品共有n件,其中m件是次品,其余为正品.现从中随机取出r件产品,
记事件Ak={取到的r件产品中恰有k件次品},则P(Ak)=
| ||||
|
显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),
因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
| ||||||||||||
|
所以
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
①等式(*)成立 ②等式(*)不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号______.
有对称中心的曲线叫做有心曲线,显然圆、椭圆、双曲线都是有心曲线.过有心曲线的中心的弦叫有心曲线的直径(为研究方便,不妨设直径所在直线的斜率存在).
定理:过圆x2+y2=r2(r>0)上异于某直径两端点的任意一点,与这条直径的两个端点连线,则两条直线的斜率之积为定值-1.写出该定理在椭圆
+
=1(a>b>0)中的推广(不必证明):
.
查看习题详情和答案>>
定理:过圆x2+y2=r2(r>0)上异于某直径两端点的任意一点,与这条直径的两个端点连线,则两条直线的斜率之积为定值-1.写出该定理在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
过椭圆
+
=1(a>b>0)上异于某直径两端点的任意一点,与这条直径的两个端点连线,则两条连线的斜率之积为定值-
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
过椭圆
+
=1(a>b>0)上异于某直径两端点的任意一点,与这条直径的两个端点连线,则两条连线的斜率之积为定值-
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
.