摘要:∴数列{cn+1}是为公比.以为首项的等比数列.
网址:http://m.1010jiajiao.com/timu_id_475689[举报]
已知f(x)=
,数列{an}是以1为首项,f(1)为公比的等比数列;数列{bn}中b1=
,且bn+1=f(bn)
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an(
-1),求{cn}的前n项和为Tn.
(3)证明:对?n∈N+,有1≤Tn<4.
查看习题详情和答案>>
| x |
| 1+x |
| 1 |
| 2 |
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an(
| 1 |
| bn |
(3)证明:对?n∈N+,有1≤Tn<4.
已知f(x)=![]() ,数列{an}为首项是1,以f(1)公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)公比的等比数列;数列{bn}中b1=![]() ,且bn+1=f(bn)
,且bn+1=f(bn)
(1)求数列{an}和{bn}的通项公式;
(2)令cn=an(![]() -1),{cn}的前n项和为Tn,证明:对
-1),{cn}的前n项和为Tn,证明:对![]() n∈N+,有1≤Tn<4
n∈N+,有1≤Tn<4
已知f(x)= ,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1= ,且bn+1=f(bn),
,且bn+1=f(bn),
(1)求数列{an}和{bn}的通项公式
(2)令 ,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
查看习题详情和答案>>
 ,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1= ,且bn+1=f(bn),
,且bn+1=f(bn),(1)求数列{an}和{bn}的通项公式
(2)令
 ,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.查看习题详情和答案>>
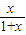 ,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1= ,且bn+1=f(bn),
,且bn+1=f(bn), ,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.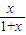 ,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1=
,数列{an}为首项是1,以f(1)为公比的等比数列;数列{bn}中b1= ,且bn+1=f(bn),
,且bn+1=f(bn),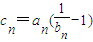 ,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.
,{cn}的前n项和为Tn,证明:对?n∈N+有1≤Tn<4.