如图，在棱长为a的正方体ABCD-

A

1

B1C1D1的面ABB₁A₁所在平面内有一点P，满足P到棱

A

1

B1所在直线的距离等于P到棱CC₁所在直线的距离，延长棱B₁B至点E，使得|B1E|=

2

|B1B|，过点E作平行于

A

1

B1的直线l交动点P的轨迹Γ于点M，N，在分别过M，N做轨迹Γ的切线交于点Q，则△MQN的面积为（　　）

（2011•洛阳二模）已知点M（-5，0），F（1，0），点K满足

MK

=2

KF

，P是平面内一动点，且满足|

PF

|•|

KF

|=

PK

•

FK

．
（1）求P点的轨迹C的方程；
（2）过点F作两条斜率存在且互相垂直的直线l₁，l₂，设l₁与曲线C相交于点A，B，l₂与曲线C相交于点D，E，求四边形ADBE的面积的最小值．

如图，抛物线C1：y2=4x的焦点到准线的距离与椭圆C2：

x2

a2

+

y2

b2

=1(a＞b＞0)的长半轴相等，设椭圆的右顶点为A，C₁，C₂在第一象限的交点为B，O为坐标原点，且△OAB的面积为

2 6

3

（1）求椭圆C₂的标准方程；
（2）过点A作直线l交C₁于C，D两点，射线OC，OD分别交C₂于E，F两点．
（I）求证：O点在以EF为直径的圆的内部；
（II）记△OEF，△OCD的面积分别为S₁，S₂，问是否存在直线l，使得S₂=3S₁？请说明理由．

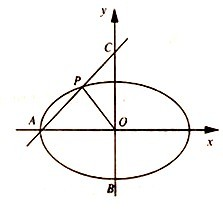在直角坐标平面xOy中，椭圆E：

x2

4

+y²=1的左顶点为A，下顶点为B．
（1）求圆心在y轴上且过两点A，B的圆方程；
（2）过点A作直线l交椭圆于点P，交y正半轴于点C，若△OAP与△OCP的面积相等，求直线l的斜率k．