摘要:在中..故.
网址:http://m.1010jiajiao.com/timu_id_473815[举报]
在 中,
中, 是三角形的三内角,
是三角形的三内角, 是三内角对应的三边,已知
是三内角对应的三边,已知 成等差数列,
成等差数列, 成等比数列
成等比数列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一问中利用依题意 且
且 ,故
,故
第二问中,由题意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,从而得到结论。
,从而得到结论。
(1)依题意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由题意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入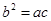 得
得

查看习题详情和答案>>
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
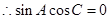

又由 得
得 即
即

又由 得
得 即
即

又
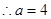 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

查看习题详情和答案>>
在交通拥挤及事故多发地段,交警要求在此地段内的安全车距d是车速v的平方与车身长S(本题中假设S为常量)乘积的正比例函数关系.已知当车速为50千米/小时,安全车距恰为车身长.为使此地段的车流量Q=
最大,则车速v=
查看习题详情和答案>>
| 1000v | d+S |
50
50
.