又PA平面PAB,平面EFG. --6分——青夏教育精英家教网——

摘要：又PA平面PAB,平面EFG. --6分

网址：http://m.1010jiajiao.com/timu_id_473740[举报]

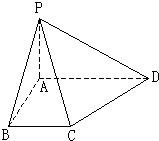如图，在底面是直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°，且∠ADC=arcsin

，又PA⊥平面ABCD，AD=3AB=3PA=3a，
（I）求二面角P-CD-A的正切值；
（II）求点A到平面PBC的距离．查看习题详情和答案>>

如图，在矩形ABCD中，AB=

，BC=a，又PA⊥平面ABCD，PA=4．
（1）若在边BC上存在点Q，且使得PQ⊥QD，求a的取值范围；
（2）当BC边上存在唯一点Q，使PQ⊥QD时，求异面直线AQ与PD所成角的大小．

查看习题详情和答案>>

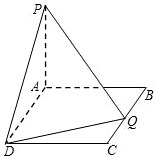如图，在矩形ABCD中，AB=2，BC=a，又PA⊥平面ABCD，PA=4．
（Ⅰ）若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；
（Ⅱ）当边BC上存在唯一点Q，使PQ⊥QD时，求二面角A-PD-Q的余弦值．查看习题详情和答案>>

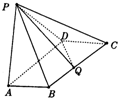如图，四棱锥P-ABCD中，底面ABCD是矩形，AB=

，BC=a，又PA⊥平面ABCD，PA=4．
（Ⅰ）若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；
（Ⅱ）若a=4，且PQ⊥QD，求二面角A-PD-Q的大小．

查看习题详情和答案>>

如图，在矩形ABCD中，AB＝2，BC＝a，又PA⊥平面ABCD，PA＝4．

（Ⅰ）若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；

（Ⅱ）当边BC上存在唯一点Q，使PQ⊥QD时，求二面角A－PD－Q的余弦值．

查看习题详情和答案>>