摘要： 一元二次方程两根.满足 求取值范围. 数学学案03 学习时间:2009-08-03 学习内容:不等式的性质 Eg1. ...试比较a.b.c大小. 解: ∴ Eg2.比较..的大小. 解:∵ ∴ ∵ ∴ ∴ Eg3.设...且和同时成立.试比较..大小. 解:易知.故或 ∴ . ∴ . ∴ Eg4. 已知对任意实数m都成立.求a的取值范围. 解:∵ 的最小值为1 ∴ . Eg5.给出四个条件:① ② ③ ④ 问其中哪些条件可以推出结论? 解:①.②.④ Eg6. 解不等式:(为字母系数) 解: (1)时.只须. (2)时.有 ∴
网址：http://m.1010jiajiao.com/timu_id_4453201[举报]
设虚数z1，z2满足z12=z2.
（1）若z1、z2是一个实系数一元二次方程的两个根，求z1、z2；
（2）若z1=1+mi（m＞0，i为虚数单位），ω=z2－2，ω的辐角主值为θ，求θ的取值范围.
查看习题详情和答案>>
设虚数z1，z2满足z12=z2.
（1）若z1、z2是一个实系数一元二次方程的两个根，求z1、z2；
（2）若z1=1+mi（m＞0，i为虚数单位），ω=z2－2，ω的辐角主值为θ，求θ的取值范围.
查看习题详情和答案>>
设复数β=x+yi（x，y∈R）与复平面上点P（x，y）对应．
（1）若β是关于t的一元二次方程t2-2t+m=0（m∈R）的一个虚根，且|β|=2，求实数m的值；
（2）设复数β满足条件|β+3|+（-1）n|β-3|=3a+（-1）na（其中n∈N*、常数a∈ (
， 3)），当n为奇数时，动点P（x、y）的轨迹为C1．当n为偶数时，动点P（x、y）的轨迹为C2．且两条曲线都经过点D(2，
)，求轨迹C1与C2的方程；
（3）在（2）的条件下，轨迹C2上存在点A，使点A与点B（x0，0）（x0＞0）的最小距离不小于
，求实数x0的取值范围．
查看习题详情和答案>>
（1）若β是关于t的一元二次方程t2-2t+m=0（m∈R）的一个虚根，且|β|=2，求实数m的值；
（2）设复数β满足条件|β+3|+（-1）n|β-3|=3a+（-1）na（其中n∈N*、常数a∈ (
| 3 |
| 2 |
| 2 |
（3）在（2）的条件下，轨迹C2上存在点A，使点A与点B（x0，0）（x0＞0）的最小距离不小于
2
| ||
| 3 |
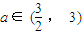），当n为奇数时，动点P（x、y）的轨迹为C1．当n为偶数时，动点P（x、y）的轨迹为C2．且两条曲线都经过点
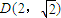，求轨迹C1与C2的方程；
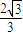，求实数x的取值范围．
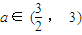），当n为奇数时，动点P（x、y）的轨迹为C1．当n为偶数时，动点P（x、y）的轨迹为C2．且两条曲线都经过点
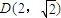，求轨迹C1与C2的方程；
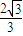，求实数x的取值范围．