摘要:3.1利用导数判断函数的单调性 学习目标: 1.正确理解利用导数判断函数的单调性的原理, 2.掌握利用导数判断函数单调性的方法 学习重点难点: 利用导数判断函数单调性. 自主学习 一.知识再现: 1. 函数的单调性. 对于任意的两个数x1.x2∈I.且当x1<x2时. 都有f(x1)<f(x2).那么函数f(x)就是区间I上的增函数. 对于任意的两个 数x1.x2∈I.且当x1<x2时.都有f(x1)>f(x2).那么函数f(x)就是区间 I上的减函数. 2. 导数的概念及其四则运算 二.新课探究: 1.定义:一般地.设函数y=f(x) 在某个区间内有导数.如果在 这个区间内0.那么函数y=f(x) 在为这个区间内的增函数,如果在 这个区间内0.那么函数y=f(x) 在为这个区间内的减函数 2.用导数求函数单调区间的步骤: ①求函数f(x)的导数f′(x). ②令f′(x) 0解不等式.得x的范围就是递增区间. ③令f′(x)0解不等式.得x的范围.就是递减区间. 3.例题解析: 例1确定函数f(x)=x2-2x+4在哪个区间内是增函数.哪个区间内是减函 数. 解:f′(x)=(x2-2x+4)′=2x-2. 令2x-2>0.解得x>1. ∴当x∈时.f′(x)>0.f(x)是增函数. 令2x-2<0.解得x<1. ∴当x∈时.f′(x)<0.f(x)是减函数. 例2确定函数f(x)=2x3-6x2+7在哪个区间内是增函数.哪个区间内是减 函数. 解:f′(x)=(2x3-6x2+7)′=6x2-12x 令6x2-12x>0.解得x>2或x<0 ∴当x∈时.f′(x)>0.f(x)是增函数. 当x∈时.f′(x)>0.f(x)是增函数. 令6x2-12x<0.解得0<x<2. ∴当x∈(0.2)时.f′(x)<0.f(x)是减函数. 例3证明函数f(x)=在上是减函数. 证法一:任取两个数x1.x2∈设x1<x2. f(x1)-f(x2)= ∵x1>0.x2>0.∴x1x2>0 ∵x1<x2.∴x2-x1>0. ∴>0 ∴f(x1)-f(x2)>0.即f(x1)>f(x2) ∴f(x)= 在上是减函数. 证法二: ∵f′(x)=( )′=(-1)·x-2=-.x>0. ∴x2>0.∴-<0. ∴f′(x)<0.∴f(x)= 在上是减函数. 例4求函数y=x2(1-x)3的单调区间. 解:y′=[x2(1-x)3]′=2x(1-x)3+x2·3(1-x)2·(-1) =x(1-x)2[2(1-x)-3x]=x(1-x)2·(2-5x) 令x(1-x)2(2-5x)>0.解得0<x<. ∴y=x2(1-x)3的单调增区间 是(0.) 令x(1-x)2(2-5x)<0.解得x<0或x>且x≠1. ∵为拐点.∴y=x2(1-x)3的单调减区间是.(.+∞) 例5.求的单调递增区间 解:由函数的定义域可知. 即 又 所以 令.得或 综上所述.的单调递增区间为(0.1) 课堂巩固: 1.函数的单调递增区间是( ) A B C D 2.已知函数.则它的单调递减区间是( ) A. B. C. D.及 3. 函数的单调递增区间是 . 4.当 时.在上是减函数. 归纳反思: 合作探究: 1.求函数的单调区间 2.已知函数的图象过点.且在点 处的切线方程为. (1)求函数的解析式,(2)求函数的单调区间. 教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记
网址:http://m.1010jiajiao.com/timu_id_4445471[举报]
已知函数 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
查看习题详情和答案>>
已知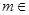 R,函数
R,函数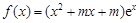 .
.
⑴若函数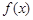 没有零点,求实数
没有零点,求实数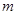 的取值范围;
的取值范围;
⑵若函数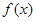 存在极大值,并记为
存在极大值,并记为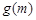 ,求
,求 的表达式;
的表达式;
⑶当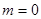 时,求证:
时,求证: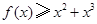 .
.
【解析】(1)求导研究函数f(x)的最值,说明函数f(x)的最大值<0,或f(x)的最小值>0.
(2)根据第(1)问的求解过程,直接得到g(m).
(3)构造函数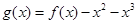 ,证明
,证明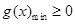 即可,然后利用导数求g(x)的最小值.
即可,然后利用导数求g(x)的最小值.
查看习题详情和答案>>
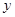 (单位:千克)与销售价格
(单位:千克)与销售价格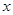 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式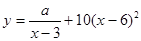 ,其中
,其中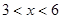 ,
,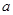 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克. (销售单价-成品单价),然后利用导数求其最值即可.
(销售单价-成品单价),然后利用导数求其最值即可.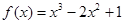 .
.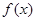 在区间
在区间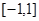 上的最大值;
上的最大值;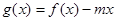 在区间
在区间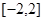 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.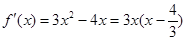 ,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在
,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在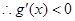 在
在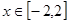 上有解,即
上有解,即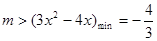 ,即可,可得到。
,即可,可得到。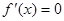 ,解得
,解得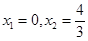 ……………3分
……………3分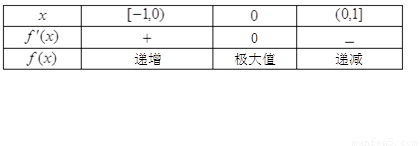
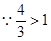 ,
,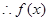 在
在 上为增函数,在
上为增函数,在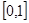 上为减函数,
上为减函数,
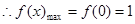 .
…………6分
.
…………6分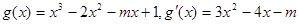
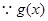 在
在 上存在递减区间,
上存在递减区间,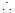
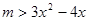 在
在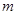 的取值范围为
的取值范围为