摘要:如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,整个轨道处于同一竖直平面内.可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道滑动.然后沿水平轨道滑行至轨道末端C处恰好没有滑出.已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失.求: (1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍. (2)物块与水平轨道BC间的动摩擦因数μ. 答案 0.3 解析 (1)设物块的质量为m,其开始下落处的位置距BC的竖直高度为h,到达B点时的速度为v,小车圆弧轨道半径为R.由机械能守恒定律,有 mgh=mv2 ① 根据牛顿第二定律,有 9mg-mg=m ② 解得h=4R ③ 即物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍. (2)设物块与BC间的滑动摩擦力的大小为F,物块滑到C点时与小车的共同速度为v′,物块在小车上由B运动到C的过程中小车对地面的位移大小为s.依题意,小车的质量为3m,BC长度为10 R.由滑动摩擦定律,有 F=μmg ④ 由动量守恒定律,有mv=v′ ⑤ 对物块.小车分别应用动能定理,有 -F=mv′2-mv2 ⑥ Fs=(3m)v′2-0 ⑦ 解得μ=0.3 ⑧
网址:http://m.1010jiajiao.com/timu_id_4439783[举报]
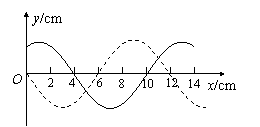 ) 如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.2 s时刻的波形图。已知该波的波速是0.8 m/s,则下列说法正确的是
) 如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.2 s时刻的波形图。已知该波的波速是0.8 m/s,则下列说法正确的是