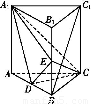
摘要：(1)证明:因为CB⊥平面A1B.所以A1C在平面A1B上的射影为A1B. 由A1B⊥AE.AE平面A1B.得A1C⊥AE. 同理可证A1C⊥AF. 因为A1C⊥AF.A1C⊥AE. 所以A1C⊥平面AEF. (2)解:过A作BD的垂线交CD于G.因为D1D⊥AG.所以AG⊥平面D1B1BD. 设AG与A1C所成的角为α.则α即为平面AEF与平面D1B1BD所成的角. 由已知.计算得DG=. 如图5-19建立直角坐标系.则得点A.G(.3.0).A1. C. AG={.3.0}.A1C={4.3.-5}. 因为AG与A1C所成的角为α. 所以cosα=. 由定理知.平面AEF与平面D1B1BD所成角的大小为arccos. 注:没有学习向量知识的同学可用以下的方法求二面角的平面角. 解法一:设AG与BD交于M.则AM⊥面BB1D1D.再作AN⊥EF交EF于N.连接MN.则∠ANM即为面AEF与D1B1BD所成的角α.用平面几何的知识可求出AM.AN的长度. 解法二:用面积射影定理cosα=. 评述:立体几何考查的重点有三个:一是空间线面位置关系的判定,二是角与距离的计算,三是多面体与旋转体中的计算.
网址：http://m.1010jiajiao.com/timu_id_4435240[举报]
如图，四棱锥S—ABCD中，SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB
(Ⅰ)证明：平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
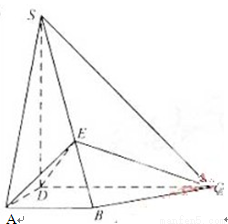
【解析】本试题主要考查了立体几何中的运用。
(1)证明：因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.，因此可知得到平面EDC⊥平面SBC.
（Ⅱ）由SA2= SD2+AD2 = 5 ，AB=1，SE=2EB，AB⊥SA，知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1，又AD=1．
故△ADE为等腰三角形．
取ED中点F，连接AF，则AF⊥DE，AF2= AD2-DF2 =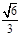
．
连接FG，则FG∥EC，FG⊥DE．
所以，∠AFG是二面角A-DE-C的平面角．
连接AG，AG= 2 ，FG2= DG2-DF2
=
，
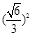cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ，
所以，二面角A-DE-C的大小为120°
查看习题详情和答案>>
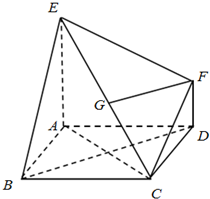如图，已知多面体EABCDF的底面ABCD是正方形，EA⊥底面ABCD，FD∥EA，且EA=2FD．（1）求证：CB⊥平面ABE；
（2）连接AC，BD交于点O，取EC中点G．证明：FG∥平面ABCD．
如图，已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（1）已知椭圆C1：
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．
