摘要:解:(1)记P(x.y).由M.N(1.0)得=-=(-1-x.-y). =-=(1-x.-y).=-=(2.0) ∴·=2(1+x).·=x2+y2-1.·=2(1-x). 于是.·.·.·是公差小于零的等差数列等价于 即 所以.点P的轨迹是以原点为圆心.为半径的右半圆. (2)点P的坐标为(x0.y0). ·=x02+y02-1=2. ||·||=. ∴cosθ=
网址:http://m.1010jiajiao.com/timu_id_4435238[举报]
设f(x)是定义在[-1,1]上的奇函数,且对任意a、b∈[-1,1],当a+b≠0时,都有
>0.
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x-
)<f(x-
);
(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围. 查看习题详情和答案>>
| f(a)+f(b) |
| a+b |
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x-
| 1 |
| 2 |
| 1 |
| 4 |
(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围. 查看习题详情和答案>>
设f(x)是定义在[-1,1]上的奇函数,且对任意a、b∈[-1,1],当a+b≠0时,都有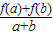 >0.
>0.
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x- )<f(x-
)<f(x- );
);
(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围.
查看习题详情和答案>>
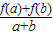 >0.
>0.(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x-
 )<f(x-
)<f(x- );
);(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围.
查看习题详情和答案>>
设f(x)是定义在[-1,1]上的奇函数,且对任意a、b∈[-1,1],当a+b≠0时,都有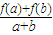 >0.
>0.
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x- )<f(x-
)<f(x- );
);
(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围.
查看习题详情和答案>>
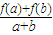 >0.
>0.(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x-
 )<f(x-
)<f(x- );
);(3)记P={x|y=f(x-c)},Q={x|y=f(x-c2)},且P∩Q=∅,求c的取值范围.
查看习题详情和答案>>
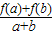 >0.
>0. )<f(x-
)<f(x- );
); >0.
>0. )<f(x-
)<f(x- );
);