摘要:(1)证明:∵.∴| |=m. 又 ∴||=m.||=m.∴△ABC为正三角形. 又·=0.即AA1⊥AB.同理AA1⊥AC.∴AA1⊥平面ABC.从而三棱柱ABC-A1B1C1是正三棱柱. (2)解:取AB中点O.连结CO.A1O. ∵CO⊥AB.平面ABC⊥平面ABB1A1.∴CO⊥平面ABB1A1.即∠CA1O为直线CA1与平面A1ABB1所成的角. 在Rt△CA1O中.CO=m.CA1=. ∴sinCA1O=.即∠CA1O=45°.
网址:http://m.1010jiajiao.com/timu_id_4435234[举报]
已知二次函数 f(x)=ax2+bx+c(a、b、c∈R)满足f(1)=1且f(-1)=0,对于任意实数x,都有f(x)≥x.
(1)证明a>0,c>0;
(2)设函数g(x)=f(x)-mx(x∈R),求m的取值范围,使函数g(x)在区间[-1,1]上是单调函数.
查看习题详情和答案>> 内有一个三棱柱ABC—A
内有一个三棱柱ABC—A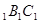 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。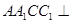 平面
平面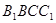 ;
; ,在圆柱OO
,在圆柱OO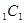
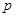 的最大值;
的最大值;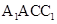 与平面
与平面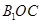 所成的角为
所成的角为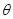
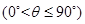 ,当
,当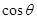 的值。
的值。