摘要:答案:-63 解析:解方程组 得 ∴a·b==-63. 评述:本题考查平面向量数量积的坐标表示及求法.
网址:http://m.1010jiajiao.com/timu_id_4435232[举报]
设函数 ,若
,若 为函数
为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是
的图象是

【答案】D
【解析】设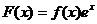 ,∴
,∴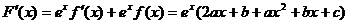 ,
,
又∴ 为
为 的一个极值点,
的一个极值点,
∴ ,即
,即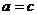 ,
,
∴ ,
,
当 时,
时, ,即对称轴所在直线方程为
,即对称轴所在直线方程为 ;
;
当 时,
时, ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.
查看习题详情和答案>>
已知:向量
=(sinx,
),
=(cosx,-1),设函数f(x)=2(
+
)•
(1)求f(x)解析式;
(2)在△ABC中,内角A,B,C的对边分别为a,b,c.若a=
,b=2,sinB=
,求f(x)+4cos(2A+
) (x∈[0,
])的取值范围.
查看习题详情和答案>>
| m |
| 3 |
| 4 |
| n |
| m |
| n |
| n |
(1)求f(x)解析式;
(2)在△ABC中,内角A,B,C的对边分别为a,b,c.若a=
| 3 |
| ||
| 3 |
| π |
| 6 |
| π |
| 2 |
 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为
| 6 | 7 |
(3)现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}(1)将“特征数”是{0,
| ||
| 3 |
y=
x-1
| ||
| 3 |
y=
x-1
; (答案写在答卷上)
| ||
| 3 |
(2)在(1)中,平移前后的两个函数分别与y轴交于A、B两点,与直线x=
| 3 |
(3)若(2)中的四边形与“特征数”是{1,-2b,b2+
| 1 |
| 2 |