摘要:数形结合是中学数学中四种重要思想方法之一.对于所研究的代数问题.有时可研究其对应几何的性质使问题得以解决,或者对于所研究的几何问题.可借助于对应图形的数量关系使问题得以解决.这种解决问题的方法称之为数形结合.1.数形结合与数形转化的目的是为了发挥形的生动性和直观性.发挥数的思路的规范性与严密性.两者相辅相成.扬长避短.
网址:http://m.1010jiajiao.com/timu_id_4433219[举报]
16、中学数学中存在许多关系,比如“相等关系”、“平行关系”等等、如果集合A中元素之间的一个关系“-”满足以下三个条件:
(1)自反性:对于任意a∈A,都有a-a;
(2)对称性:对于a,b∈A,若a-b,则有b-a;
(3)对称性:对于a,b,c∈A,若a-b,b-c,则有a-c、
则称“-”是集合A的一个等价关系、例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立)、请你再列出两个等价关系:
查看习题详情和答案>>
(1)自反性:对于任意a∈A,都有a-a;
(2)对称性:对于a,b∈A,若a-b,则有b-a;
(3)对称性:对于a,b,c∈A,若a-b,b-c,则有a-c、
则称“-”是集合A的一个等价关系、例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立)、请你再列出两个等价关系:
答案不唯一,如“图形的全等”、“图形的相似”、“非零向量的共线”、“命题的充要条件”等等
.中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合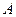 中元素之间的一个关系“
中元素之间的一个关系“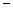 ”满足以下三个条件:
”满足以下三个条件:
(1)自反性:对于任意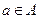 ,都有
,都有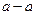 ;
;
(2)对称性:对于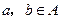 ,若
,若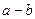 ,则有
,则有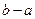 ;
;
(3)传递性:对于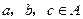 ,若
,若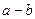 ,
,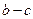 ,则有
,则有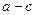 .
.
则称“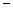 ”是集合
”是集合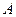 的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.如果集合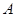 中元素之间的一个关系“
中元素之间的一个关系“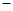 ”满足以下三个条件:
”满足以下三个条件:
(1)自反性:对于任意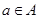 ,都有
,都有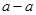 ;
;
(2)对称性:对于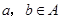 ,若
,若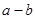 ,则有
,则有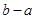 ;
;
(3)传递性:对于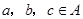 ,若
,若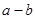 ,
,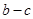 ,则有
,则有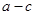 .
.
则称“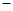 ”是集合
”是集合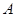 的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
查看习题详情和答案>>