网址:http://m.1010jiajiao.com/timu_id_431530[举报]
一、选择题:本题考查基础知识和基本运算. 每题5分,满分50分.
1. B 2.A 3.D 4.D 5.C 6.B 7.D 8.A 9.B 10.C
二、填空题:本题考查基础知识和基本运算. 每题4分,满分20分.
11. 31 12. 15 13. 16 14. 4
15. 16+17+18+19=12+13+14+15+16=7+8+9+10+11+12+13.
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
.files/image224.gif) 16.本题主要考查频率分布表、直方图、众数、分层抽样、分布列、期望等统计概率知识,考查学生运用所学知识解决实际应用问题的能力。满分13分.
16.本题主要考查频率分布表、直方图、众数、分层抽样、分布列、期望等统计概率知识,考查学生运用所学知识解决实际应用问题的能力。满分13分.
解:(I)①处填20,②处填0.35;
众数为
补全频率分布直方图如图所示。
…………6分
(Ⅱ)用分层抽样的方法,从中选
取20人,则其中“身高低于
的有5人,“身高不低于
的有15人。 ……7分
故ξ的可能取值为0,1,2,3;
.files/image226.gif)
.files/image228.gif)
.files/image230.gif)
.files/image232.gif) …………………10分
…………………10分
所以ξ的分布列为
ξ
0
1
2
3
P
.files/image234.gif)
.files/image236.gif)
.files/image238.gif)
.files/image240.gif)
…………11分
所以:.files/image242.gif) …………13分
…………13分
.files/image246.gif) 17. 本题主要考查三视图,线面位置关系,二面角的求法等基本知识,考查空间想像能力,探索运算求解能力和推理论证能力. 满分13分.
17. 本题主要考查三视图,线面位置关系,二面角的求法等基本知识,考查空间想像能力,探索运算求解能力和推理论证能力. 满分13分.
法一:(Ⅰ)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
∴BA,BC,BB1两两垂直.
以BA,BC,BB1分别为x,y,z轴建立空间直角坐标系,……1分
则N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4)
∵.files/image248.gif) =(4,4,0)?(-4,4,0)=-16+16=0
=(4,4,0)?(-4,4,0)=-16+16=0
.files/image250.gif) =(4,4,0)?(0,0,4)=0
……3分
=(4,4,0)?(0,0,4)=0
……3分
∴BN⊥NB1, BN⊥B.files/image252.jpg)
∴BN⊥平面C1B1N; ……4分
(Ⅱ)∵BN⊥平面C1B1N, .files/image254.gif) 是平面C1B1N的一个法向量
是平面C1B1N的一个法向量.files/image256.gif) =(4,4,0),
……5分
=(4,4,0),
……5分
设.files/image258.gif) =(x,y,z)为平面NCB1的一个法向量,
=(x,y,z)为平面NCB1的一个法向量,
则.files/image260.gif)
.files/image262.gif)
.files/image264.gif)
.files/image262.gif)
.files/image266.gif) ,取
,取.files/image258.gif) =(1,1,2), …7分
=(1,1,2), …7分
则cosθ=.files/image268.gif) =
=.files/image270.gif) =
=.files/image272.gif) ;
……9分
;
……9分
(Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,则.files/image274.gif) =(-2,0,a),∵MP∥平面CNB1,
=(-2,0,a),∵MP∥平面CNB1,
∴.files/image274.gif) ⊥
⊥.files/image258.gif)
.files/image262.gif)
.files/image274.gif) ?
?.files/image258.gif) =(-2,0,a) ?(1,1,2)=-2+
=(-2,0,a) ?(1,1,2)=-2+.files/image262.gif) a
a
.files/image276.gif) 又MP
又MP.files/image278.gif) 平面CNB1, ∴MP∥平面CNB1, ∴当BP=1时MP∥平面CNB1. ……13分
平面CNB1, ∴MP∥平面CNB1, ∴当BP=1时MP∥平面CNB1. ……13分
法二:(Ⅰ)证明:由已知得B
BN=4.files/image280.gif) = B1N,BB1=8, ∴BB12= BN2+ B1N2, ∴BN⊥B1N
= B1N,BB1=8, ∴BB12= BN2+ B1N2, ∴BN⊥B1N
又B
(Ⅱ)过N作NQ.files/image282.gif) B
B.files/image284.gif) BCQN,又BN⊥平面C1B1N,
BCQN,又BN⊥平面C1B1N,
.files/image286.gif) ∴CQ⊥平面C1B1N,则CQ⊥B1N, QN⊥B1N ,∴∠CNQ是二面角C-B1N-Q的平面角θ,
∴CQ⊥平面C1B1N,则CQ⊥B1N, QN⊥B1N ,∴∠CNQ是二面角C-B1N-Q的平面角θ,
在Rt△CNQ中,NQ=4,CQ=4.files/image280.gif) , ∴CN=4
, ∴CN=4.files/image062.gif) ,cosθ=
,cosθ=.files/image289.gif) =
=.files/image272.gif) ;
;
(Ⅲ)延长BA、B1N交于R,连结CR,∵MP∥平面CNB1,
MP.files/image292.gif) 平面CBR, 平面CBR∩平面CRN于CR,
平面CBR, 平面CBR∩平面CRN于CR,
∴MP∥CR, △RB1B中AN.files/image282.gif)
.files/image294.gif) BB1,∴A为RB中点,
BB1,∴A为RB中点,
∴.files/image296.gif) =
=.files/image298.gif) =
=.files/image300.gif) ,∴BP=1,因此存在P点使MP∥平面CNB1.
……………13分
,∴BP=1,因此存在P点使MP∥平面CNB1.
……………13分
.files/image305.gif) 18.本题主要考查学生运用正弦和余弦定理解决与三角形有关的实际问题的能力,考查学生的运算能力以及化归与转化的数学思想方法。满分13分.
18.本题主要考查学生运用正弦和余弦定理解决与三角形有关的实际问题的能力,考查学生的运算能力以及化归与转化的数学思想方法。满分13分.
法一:1、在△ABC中,∵∠BAD=90°,∠ABD=45°,∴∠ADB=45°…2分
.files/image307.gif) ……………………4分
……………………4分
在.files/image309.gif) 中,
中,.files/image311.gif)
.files/image313.gif) ……………6分
……………6分.files/image252.jpg)
在.files/image315.gif) 中,DC2=DB2+BC2-2DB?BCcos60°=(80
中,DC2=DB2+BC2-2DB?BCcos60°=(80.files/image280.gif) )2+(40
)2+(40.files/image280.gif) )2-2×80
)2-2×80.files/image280.gif) ×40
×40.files/image280.gif) ×
×.files/image294.gif)
=9600 ……………10分
.files/image319.gif) ………………11分
………………11分
航模的速度.files/image321.gif) (米/秒)
……………12分
(米/秒)
……………12分
答:航模的速度为2.files/image323.gif) (米/秒)
……………13分
(米/秒)
……………13分
法二:(略解)、在.files/image325.gif) 中,
中,.files/image327.gif) 中
中.files/image329.gif)
在 .files/image331.gif) 中,DC2=AD2+AC2-2AD?ACcos60°=9600
……………10分
中,DC2=AD2+AC2-2AD?ACcos60°=9600
……………10分
.files/image334.gif)
.files/image335.gif) ……………11分
……………11分
航模的速度.files/image321.gif) (米/秒) ………12分
(米/秒) ………12分
答:航模的速度为2.files/image323.gif) (米/秒) ……………13分
(米/秒) ……………13分
法三:(略解)、如图建立直角坐标系,
则A(0,0), B(80,0), D(0,80) …………2分
由.files/image309.gif) ,AC=40(1+
,AC=40(1+.files/image338.gif) ),∴C(60+20
),∴C(60+20.files/image338.gif) ,20+20
,20+20.files/image338.gif) )
……………7分
)
……………7分
.files/image340.gif) ……………11分
……………11分
航模的速度.files/image321.gif) (米/秒)
……………12分
(米/秒)
……………12分
答:航模的速度为2.files/image323.gif) (米/秒) ……………13分
(米/秒) ……………13分
19、本题主要考查直线、圆与椭圆的位置关系等基本知识,考查运算求解能力和探索求解、分析问题、解决问题的能力. 满分13分
解: (Ⅰ) 设C(x, y), ∵ .files/image342.gif) ,
, .files/image344.gif) , ∴
, ∴ .files/image346.gif) ,
,
∴ 由定义知,动点C的轨迹是以A、B为焦点,长轴长为6的椭圆,除去与x轴的两个交点.
设椭圆方程为.files/image348.gif)
则a=3,c=2.∴b2=a2-c2=5.∴ 曲线M的方程为: .files/image350.gif) (y≠0).(缺y≠0的扣1分)……5分
(y≠0).(缺y≠0的扣1分)……5分
.files/image351.gif) (Ⅱ)法一: 即要使DE⊥DF, 用特值法kDE=1,
(Ⅱ)法一: 即要使DE⊥DF, 用特值法kDE=1,
由.files/image353.gif) 得14y2+30y=0,又y≠0, ∴y=-
得14y2+30y=0,又y≠0, ∴y=-.files/image355.gif) ,代入DE得x=
,代入DE得x=.files/image357.gif) ,
,
由对称性知定点在x轴上, ∴最多只有定点Q.files/image359.gif) ……8分
……8分
设直线DE的方程为x=my+3,E(x1,y1),
由.files/image361.gif) 得(
得(.files/image363.gif)
∴E(.files/image365.gif) ,-
,-.files/image363.gif) ),
…………………10分
),
…………………10分
同理F(.files/image367.gif) ,
,.files/image369.gif) )
…………………11分
)
…………………11分
kQE-kQF=.files/image371.gif) -
-.files/image373.gif) =
=.files/image375.gif) -
-.files/image375.gif) =0
=0
得E、Q、F三点共线,得出定点坐标为.files/image359.gif) .
…………………13分
.
…………………13分
法二:当直线l的斜率存在时,设直线l的方程为yx=kx+m,E(x1,y1),F(x1,y1),
由.files/image378.gif) 得
得.files/image380.gif) ,
,
由△=(18mk)2-36(5+9k2)(m2-5)>0, 得5+9k2- m2>0,
.files/image382.gif) ………………………8分
………………………8分
又.files/image384.gif) ,
,
因为以EF为直径的圆过点.files/image386.gif) 等价于
等价于.files/image388.gif) ,即
,即.files/image390.gif)
.files/image392.gif) ,
,.files/image394.gif) ,
,
.files/image396.gif) .解得:
.解得:.files/image398.gif) ,
,.files/image400.gif) ,且均满足
,且均满足.files/image402.gif) ,
,
当m1=-3k时,l的方程为y=k(x-3),直线过点Q(3,0),因为点Q不在曲线M上,此时l与曲线M没有两个公共点,不合题意;
当.files/image404.gif) 时,
时,.files/image197.gif) 的方程为
的方程为.files/image407.gif) ,直线过定点
,直线过定点.files/image359.gif) . ……………11分
. ……………11分
当直线l的斜率不存在时,直线.files/image410.gif) 与曲线M交于
与曲线M交于.files/image412.gif) 两点,此时
两点,此时
.files/image414.gif) ,由
,由.files/image388.gif) ,得
,得.files/image416.gif) ,点
,点.files/image418.gif) 在曲线M上,
在曲线M上,.files/image420.gif) ,所以
,所以.files/image422.gif) ,解得
,解得.files/image424.gif) ,即直线
,即直线 .files/image426.gif) 满足条件.
满足条件.
∴直线.files/image197.gif) 过定点,定点坐标为
过定点,定点坐标为.files/image359.gif) .
……………………………13分
.
……………………………13分
20. 本题主要考查函数、导数的基本知识及用导数处理函数性质,递推数列及不等式、数学归纳法等基础知识,同时考查考生函数与方程思想、分类与整合思想、化归与转化思想等及推理论证能力、运算求解能力及创新意识.满分14分.
解: (Ⅰ)f '(x)= .files/image199.gif) -
-.files/image429.gif) ,又函数f(x)在x=1处有极值,∴f '(1)=0,a=1,经检验符合题意 ……2分
,又函数f(x)在x=1处有极值,∴f '(1)=0,a=1,经检验符合题意 ……2分
g'(x)= .files/image199.gif) -
-.files/image431.gif) ,
,
当x∈(0,1)时, g'(x)<0, g(x)为减函数, 当x =1时,g'(x)=0, 当x∈(1,+∞)时g'(x)>0,g(x)为增函数,∴g(x)在x =1时取得极小值g(1)=2+b,依题意g(1)≤0, ∴b≤-2,
∴b的最大值为-2; ………………………………………………4分
(Ⅱ)f '(x)= .files/image199.gif) -
-.files/image429.gif) ,
,.files/image252.jpg)
当f (x)在(1,2)上单调递增时, .files/image199.gif) -
-.files/image429.gif) ≥0在[1,2]上恒成立, ∴a ≤x2
≥0在[1,2]上恒成立, ∴a ≤x2.files/image199.gif) ,令h(x)= x2
,令h(x)= x2.files/image199.gif) ,
,
则h'(x)= .files/image199.gif) ( x2+2 x)>0在[1,2]上恒成立,
即h(x) 在[1,2]上单调递增,
( x2+2 x)>0在[1,2]上恒成立,
即h(x) 在[1,2]上单调递增,
∴h(x) 在[1,2]上的最小值为h(1)=1, ∴a≤1; ……………………………………7分
当f(x)在[1,2]上单调递减时,同理a≥x2
(本小题满分13分)
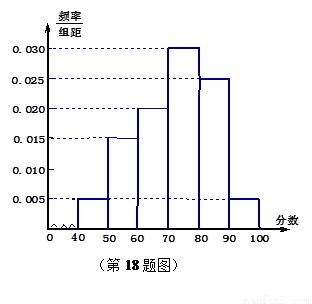
从某校高一年级参加期末考试的学生中抽出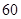 名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)根据频率分布直方图估计这次考试该年级的数学平均分;
(2) 已知在[90,100]内的学生的数学成绩都不相同,且都在95分以上(不含95分),现用简单随机抽样方法,从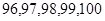 这
这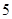 个数中任取
个数中任取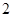 个数,求这
个数,求这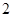 个数恰好是两名学生的数学成绩的概率.
个数恰好是两名学生的数学成绩的概率.
 |
查看习题详情和答案>>
(本小题满分13分)
在某次测验中,有6位同学的平均成绩为75分。用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率。
查看习题详情和答案>>(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件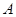 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率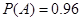 .
.
(1)求从该批产品中任取1件是二等品的概率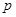 ;
;
(2)若该批产品共100件,从中任意抽取2件,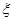 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求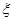 的分布列.
的分布列.
查看习题详情和答案>>

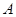 :“取出的2件产品都是二等品”的概率
:“取出的2件产品都是二等品”的概率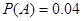
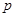 ;
;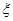 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求