网址:http://m.1010jiajiao.com/timu_id_430624[举报]
一、 选择题: DCCBC ABAAD BB
二、 填空题:13.  ;14.
;14.  ;15.
;15.  ;16.
;16.
三、 解答题:
17.(10分)解:(Ⅰ)由已知得
由余弦定理得 ,即
,即 …………………………3分
…………………………3分
因为锐角△ABC中,A+B+C=p, ,所以
,所以 ,则
,则
 ………………………6分
………………………6分
(Ⅱ) ,则
,则 .将
.将 ,
, 代入余弦定理:
代入余弦定理: 得
得 解得
解得 .…10分
.…10分
18. (12分)解:(Ⅰ)依题意,当甲连胜 局或乙连胜
局或乙连胜 局时,第二局打完时比赛结束.
局时,第二局打完时比赛结束.
 有
有 . 解得
. 解得 或
或 .
.  ,
,  .…6分
.…6分
(Ⅱ)根据比赛规则可知,若恰好打满4局后比赛结束,必须是前两局打成平局,第三、第四局只能甲全胜或乙全胜.所求概率P= …………………12分
…………………12分
19.(12分)解:(Ⅰ) ,
, 面
面 ,
,
 ,又
,又 ,
,
 面
面 . …………………………………………………………6分
. …………………………………………………………6分
(Ⅱ)过 作
作 垂足为
垂足为 ,则
,则 .
.
过 作
作 ,垂足为
,垂足为 ,连结EF由三垂线定理得
,连结EF由三垂线定理得 ;
;

 是所求二面角
是所求二面角 的平面角.……………………9分
的平面角.……………………9分
设, ,
,
在 中,由
中,由 ,
,
得 ,所以
,所以 .
.
在 中,
中, ,
, ,
,

故所求二面角 的为
的为 .…………………………………………12分
.…………………………………………12分
20(12分)解: (Ⅰ) …………2分
…………2分
∵ 在区间
在区间 上是增函数
上是增函数
∴ …………4分
…………4分
(Ⅱ)∵ 且
且 ∴对称轴为
∴对称轴为 …………6分
…………6分
∴当 时
时 取到最大值
取到最大值 ∴
∴ ∴
∴ …………8分
…………8分
∴
∴ 的增区间为
的增区间为 减区间为
减区间为 …………12分
…………12分
21.(12分)
解:(Ⅰ)由题意知,
易得 ………………………………4分
………………………………4分
(Ⅱ)



∴当 时,
时, ,
,
当 ………………8分
………………8分
∴当 时,
时, 取最大值是
取最大值是 ,又
,又
 ,即
,即 ………………12分
………………12分
22. (12分) 解:(Ⅰ)由题意:∵|PA|=|PB|且|PB|+|PF|=r=8
∴|PA|+|PF|=8>|AF| ∴P点轨迹为以A、F为焦点的椭圆…………………………2分
设方程为

(Ⅱ)假设存在满足题意的直线l,若l斜率不存在,易知
不符合题意,故其斜率存在,设为k,设


 ………6分
………6分

 ………8分
………8分
 ………10分
………10分
解得 代入验证
代入验证 成立
成立

 ………12分
………12分
| m |
| n |
| m |
| n |
| ||
| 2 |
(1)求∠B的大小;
(2)若b=3,求a+c的最大值.
 =(sinA,cosA),
=(sinA,cosA), =(cosC,sinC),且
=(cosC,sinC),且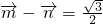 .
.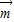 =(sinA,cosA),
=(sinA,cosA),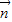 =(cosC,sinC),且
=(cosC,sinC),且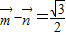 .
.