摘要：∴C1N⊥侧面BB1C1C. 面C1NB ------12∴截面C1NB⊥侧面BB1C1C. ∴截面MBC1⊥侧面BB1C1C. ------14统一:立体几何证明过程中推理缺少条件的每个扣1分补想法:(Ⅲ) AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗? 请你叙述判断理由．(Ⅲ)解: 结论是肯定的, 充分性已由(2)证明． 下面证必要性: 过M作ME⊥B C1于E, ∵截面MBC1⊥侧面BB1C1C,∴ME⊥侧面BB1C1C. 又∵AD⊥侧面BB1C1C, ∴ME∥AD.∴M, E, A, D共线. ∵A M∥侧面BB1C1C, ∴AM∥DE. ∵CC1⊥AM,∴DE∥CC1. ∵D是BC的中点, ∴E是BC1的中点.
网址：http://m.1010jiajiao.com/timu_id_430241[举报]
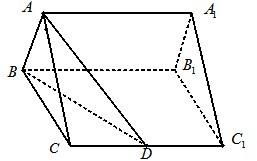如图，已知正三棱柱ABC-A1B1C1的底面正三角形的边长是2，D是CC1的中点，直线AD与侧面BB1C1C所成的角是45°．（1）求二面角A-BD-C的大小；
（2）求点C到平面ABD的距离． 查看习题详情和答案>>
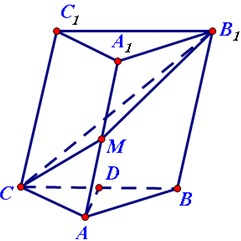在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．D为BC的中点，M为AA1的中点．（1）求证：AD∥平面MB1C；
（2）求证：平面MB1C⊥侧面BB1C1C． 查看习题详情和答案>>
（2012•潍坊二模）如图，斜三棱柱ABC-A1B1C1，侧面BB1C1C⊥底面ABC，△BC1C是等边三角形，AC⊥BC，AC=BC=4．（1）求证：AC⊥B
| C | 1 |
（2）设D为BB1的中点，求二面角D-AC-B的余弦值．
如图，斜三棱柱ABC-A1B1C1，已知侧面BB1C1C与底面ABC垂直且∠BCA=90°，∠B1BC=60°，BC=BB1=2，若二面角A-B1B-C为30°．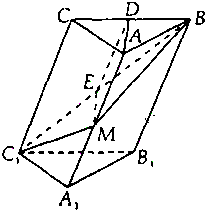
在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC．