摘要:注:求出z1后.z3=iz1=
网址:http://m.1010jiajiao.com/timu_id_425925[举报]
是否存在这样的平移,使抛物线y=-x2平移后过原点,且以平移后的抛物线的顶点和它与x轴的两个交点为顶点的三角形的面积为1?若不存在,请说明理由;若存在,求出平移后抛物线的解析式.
查看习题详情和答案>>
17.求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积![]() 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为![]() ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为![]() ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
试给出问题“在平面直角坐标系![]() 中,求点
中,求点![]() 到直线
到直线![]() 的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
的距离.”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
已知抛物线C:y2=2px(p>0)上任意一点到焦点F的距离比到y轴的距离大1.
(1)求抛物线C的方程;
(2)若过焦点F的直线交抛物线于M、N两点,M在第一象限,且|MF|=2|NF|,求直线MN的方程;
(3)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.
例如,原来问题是“若正四棱锥底面边长为4,侧棱长为3,求该正四棱锥的体积”.求出体积 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
现有正确命题:过点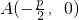 的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.
的直线交抛物线C:y2=2px(p>0)于P、Q两点,设点P关于x轴的对称点为R,则直线RQ必过焦点F.
试给出上述命题的“逆向”问题,并解答你所给出的“逆向”问题.
查看习题详情和答案>>
在自然条件下,一年中10次测量的某种细菌一天内存活时间的统计表(时间近似到0.1小时)如下表所示:
| 日期 | 1月 1日 | 2月 28日 | 3月 21日 | 4月 27日 | 5月 27日 | 6月 21日 | 8月 13日 | 9月 20日 | 10月 25日 | 12月 21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 263 | 298 | 355 |
| 存活时间y(小时) | 5.6 | 10.2 | 12.3 | 16.4 | 17.3 | 19.4 | 16.4 | 12.5 | 8.5 | 5.4 |
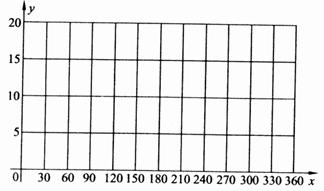
(1) 以日期在365天中的位置序号为横坐标,一天内存活时间为纵坐标,在给定坐标系中画出这些数据的散点图.
(2) 试选用一个形如![]() +t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
+t的函数来近似描述一年中该细菌一天内的存活时间y与日期位置序号x之间的函数关系.(注:①求出所选用的函数关系式;②一年按365天计算)
(3) 用(2)中的函数模型估计该种细菌一年中大约有多少天的存活时间大于15.9小时.
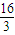 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为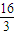 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为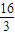 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.