摘要:于是,所以选B.
网址:http://m.1010jiajiao.com/timu_id_425746[举报]
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4-4坐标系与参数方程)将参数方程
|
B.(选修4-5 不等式选讲)不等式|x-1|+|2x+3|>5的解集是
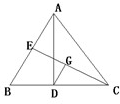
C.(选修4-1 几何证明选讲)如图,在△ABC中,AD是高线,CE是中线,|DC|=|BE|,DG⊥CE于G,且|EC|=8,则|EG|=
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)A.(不等式选做题)
已知a∈R,若关于x的方程x2+4x+|a-1|+|a+1|=0无实根,则a的取值范围是
(-∞,-2)∪(2,+∞)
(-∞,-2)∪(2,+∞)
.B.(几何证明选做题)
如图,CD是圆O的切线,切点为C,点A、B在圆O上,BC=1,∠BCD=30°,则圆O的面积为
π
π
.C.(坐标系与参数方程选做题)
在极坐标系中,若过点(1,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=
2
| 3 |
2
.| 3 |
 选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准)
选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准)(a) 不等式|x-4|-|x-2|>1的解集为
(-∞,
)
| 5 |
| 2 |
(-∞,
)
.| 5 |
| 2 |
(b) 已知直线l的极坐标方程为:ρcosθ-ρsinθ-
| 2 |
|
相切
相切
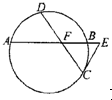
.(c) 如图已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=
| 2 |
| ||
| 2 |
| ||
| 2 |
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)(A)(坐标系与参数方程选做题)在直角坐标系x0y中,以原点为极点,x轴非负半轴为极轴建立极坐标系,已知圆C与直线l的方程分别为:ρ=2sinθ,
|
-1
-1
.(B)(不等式选做题)若关于x的不等式|x-m|<2成立的充分不必要条件是2≤x≤3,则实数m的取值范围是
(1,4)
(1,4)
.(C) (几何证明选讲) 如图,割线PBC经过圆心O,OB=PB=1,OB绕点O逆时针旋转120°到OD,连PD交圆O于点E,则PE=
3
| ||
| 7 |
3
| ||
| 7 |
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)