网址:http://m.1010jiajiao.com/timu_id_410803[举报]
一、选择题:本大题12个小题,每小题5分,共60分.
BBDDC DA CDA CA
二、填空题:本大题共4个小题,每小题4分,共16分.
13、i≥11,或i>10;
14、2 ; 15、2 ;16.①②.files/image168.gif) ③④
①③
③④
①③.files/image168.gif) ②④
②④
三、解答题:本大题共6个小题,满分74分.
=.files/image181.gif)
=.files/image183.gif) …………………………4分
…………………………4分
(1)由题意可知.files/image185.gif) ,∴
,∴.files/image187.gif) 又
又.files/image137.gif) >1,∴0≤
>1,∴0≤.files/image137.gif) ≤1
……………………6分
≤1
……………………6分
∵x∈.files/image196.gif) ………………8分
………………8分
从而当2x-.files/image193.gif) =
=.files/image193.gif) 即x=
即x=.files/image193.gif) 时fmax(x)=f(
时fmax(x)=f(.files/image193.gif) )=sin
)=sin.files/image193.gif) +k+
+k+.files/image146.gif) =k+1=
=k+1=.files/image146.gif)
∴k=-.files/image146.gif) 故f (x)=sin(2x-
故f (x)=sin(2x-.files/image193.gif) )…………………12分
)…………………12分
18、(本小题满分12分)由a、b、c成等差数列
得a+c=2b 平方得a2+c2=4b2-
又S△ABC=.files/image150.gif) 且sin B=
且sin B=.files/image148.gif) , ∴S△ABC=
, ∴S△ABC=.files/image146.gif) ac? sin B=
ac? sin B=.files/image146.gif) ac×
ac×.files/image148.gif) =
=.files/image203.gif) ac=
ac=.files/image150.gif)
故ac=.files/image205.gif) ②………………………………………………………………………4分
②………………………………………………………………………4分
由①②可得a2+c2=4b2-.files/image207.gif) ③…………………………………………………5分
③…………………………………………………5分
又∵sin B=.files/image148.gif) ,且a、b、c成等差数列∴cos B=
,且a、b、c成等差数列∴cos B=.files/image209.gif) =
=.files/image211.gif) =
=.files/image213.gif) …………8分
…………8分
由余弦定理得: b2=a2+c2-.files/image205.gif) ×
×.files/image213.gif) =a2+c2-
=a2+c2-.files/image216.gif) ④………10分
④………10分
由③④可得 b2=4∴b=2………………….…12分
19、略解:(Ⅰ)∵数列{an}的前n项和为.files/image152.gif) ∴a1= S1=1…………(1分)
∴a1= S1=1…………(1分)
当n≥2时,an= Sn- Sn-1=n………………(3分) ∴an=n………………(4分)
(Ⅱ)由若b1=1,2bn-bn-1=0得.files/image218.gif) …………(5分)
…………(5分)
∴{bn}是以b1=1为首项,1/2为公比的等比数列. …………(6分)
.files/image220.gif) …………(8分) ∴
…………(8分) ∴.files/image222.gif) ………(9分)
………(9分)
.files/image224.gif) ………(10分)
………(10分)
两式相减得: .files/image226.gif) ………(11分)
………(11分)
∴ Tn<4………(12分)
20、解:(I)将圆C配方得:(x+1)2+(y-2)2=2………………(1分)
.files/image228.gif)
.files/image230.gif)
.files/image232.gif) 21、解:(1)
21、解:(1).files/image234.gif) Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长.files/image238.gif) ,半焦距
,半焦距.files/image240.gif) ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是.files/image242.gif) ……4分
……4分
(2)因为.files/image244.gif) ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若l的斜率不存在,直线l的方程为x=2,由.files/image252.gif)
.files/image254.gif) 矛盾,故l的斜率存在. …………6分
矛盾,故l的斜率存在. …………6分
设l的方程为.files/image256.gif)
.files/image258.gif)
.files/image264.gif) ② …………10分
② …………10分
把①、②代入.files/image266.gif) ∴存在直线
∴存在直线.files/image268.gif) 使得四边形OASB的对角线相等.
…12分
使得四边形OASB的对角线相等.
…12分
22、解:(Ⅰ) .files/image270.gif)
因为函数f(x)在区间[-1,1]上是增函数,所以f‘(x)≥0在区间x∈[-1,1]恒成立
即有x2-ax-2≤0在区间[-1,1]上恒成立。 构造函数g(x)=x2-ax-2
∴满足题意的充要条件是:.files/image272.gif)
所以所求的集合A[-1,1] ………(7分)
(Ⅱ)由题意得:.files/image274.gif) 得到:x2-ax-2=0………(8分)
得到:x2-ax-2=0………(8分)
因为△=a2+8>0
所以方程恒有两个不等的根为x1、x2由根与系数的关系有:.files/image276.gif) ……(9分)
……(9分)
因为a∈A即a∈[-1,1],所以.files/image278.gif) 要使不等式
要使不等式.files/image166.gif) 对任意a∈A及t∈[-1,1]恒成立,当且仅当
对任意a∈A及t∈[-1,1]恒成立,当且仅当.files/image280.gif) 对任意的t∈[-1,1]恒成立……(11分)
对任意的t∈[-1,1]恒成立……(11分)
构造函数φ(x)=m2+tm-2=mt+(m2-2) ≥0对任意的t∈[-1,1]恒成立的充要条件是
.files/image282.gif) m≥2或m≤-2.故存在实数m满足题意且为
m≥2或m≤-2.故存在实数m满足题意且为
{m| m≥2或m≤-2}为所求 (14分)
本资料由《七彩教育网》www.7caiedu.cn 提供!
(本小题满分14分)已知函数![]() (x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程
(x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A(Ⅱ)设关于x的方程![]() 的两实数根为x1、x2.
的两实数根为x1、x2.
试问:
是否存在实数m,使得不等式![]() 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
(本小题满分14分)已知函数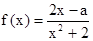 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值所组成的集合A;
(Ⅱ)设关于x的方程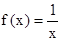 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式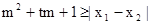 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
查看习题详情和答案>>
 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.(Ⅰ)求实数a的值所组成
 的集合A;
的集合A;(Ⅱ)设关于x的方程
 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? .files/image129.gif)
.files/image172.gif)
.files/image133.gif)
.files/image135.gif)
.files/image177.gif)
.files/image179.gif)
.files/image191.gif)
.files/image246.gif)
.files/image248.gif)
.files/image250.gif)
.files/image260.gif) ①
①.files/image262.gif)
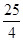 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.