摘要:当时..∴函数在(.+)上是增函数,
网址:http://m.1010jiajiao.com/timu_id_390511[举报]
已知函数f (x)=alnx+x2 (a为实常数).
(Ⅰ)若a=-2,求证:函数f (x)在(1,+∞)上是增函数;
(Ⅱ)求函数f (x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若当x∈[1,e]时,f (x)≤(a+2)x恒成立,求实数a的取值范围.
查看习题详情和答案>>探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
函数f(x)=x+ (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;
(1)函数f(x)=x+ (x>0)在区间 上递增.
(x>0)在区间 上递增.
当x= 时,y最小= .
(2)证明:函数f(x)=x+ 在区间(0,2)上递减.
在区间(0,2)上递减.
(3)思考:函数f(x)=x+ (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)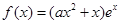 ,其中e是自然数的底数,
,其中e是自然数的底数,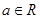 .
.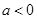 时,解不等式
时,解不等式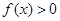 ;
; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程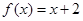 在[k,k+1]上有解;
在[k,k+1]上有解;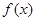 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求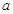 的取值范围.
的取值范围.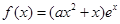 ,其中e是自然数的底数,
,其中e是自然数的底数, .
. 时,解不等式
时,解不等式 ;
; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解;
在[k,k+1]上有解; 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围.
的取值范围.