摘要：定义在D上的函数.如果满足:对.常数B.都有≤B成立.则称函数在D上有上界.其中B称为函数的上界. -----7分
网址：http://m.1010jiajiao.com/timu_id_390501[举报]
定义在D上的函数，如果满足：存在常数M＞0，对任意x∈D都有|f（x）|≤M成立，则称f（x）是D上的有界函数．
（1）试判断函数f(x)=2sin(x+
)+3在实数集R上，函数g(x)=x3+
在[
，3]上是不是有界函数？若是，请给出证明；若不是，请说出理由．
（2）若已知某质点的运动距离S与时间t的关系为S(t)=
t4+3lnt-at，要使在t∈[
，3]上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．
查看习题详情和答案>>
（1）试判断函数f(x)=2sin(x+
| π |
| 6 |
| 3 |
| x |
| 1 |
| 3 |
（2）若已知某质点的运动距离S与时间t的关系为S(t)=
| 1 |
| 4 |
| 1 |
| 3 |
定义在D上的函数，如果满足：存在常数M＞0，对任意x∈D都有|f（x）|≤M成立，则称f（x）是D上的有界函数．
（1）试判断函数f(x)=2sin(x+
)+3在实数集R上，函数g(x)=x3+
在[
，3]上是不是有界函数？若是，请给出证明；若不是，请说出理由．
（2）若已知某质点的运动距离S与时间t的关系为S(t)=
t4+3lnt-at，要使在t∈[
，3]上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．
查看习题详情和答案>>
（1）试判断函数f(x)=2sin(x+
| π |
| 6 |
| 3 |
| x |
| 1 |
| 3 |
（2）若已知某质点的运动距离S与时间t的关系为S(t)=
| 1 |
| 4 |
| 1 |
| 3 |
定义在D上的函数，如果满足：存在常数M＞0，对任意x∈D都有|f（x）|≤M成立，则称f（x）是D上的有界函数．
（1）试判断函数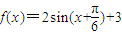
在实数集R上，函数
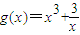在
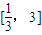上是不是有界函数？若是，请给出证明；若不是，请说出理由．
（2）若已知某质点的运动距离S与时间t的关系为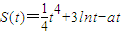
，要使在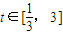
上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．
查看习题详情和答案>>
（1）试判断函数
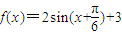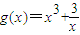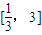在实数集R上，函数在上是不是有界函数？若是，请给出证明；若不是，请说出理由．（2）若已知某质点的运动距离S与时间t的关系为
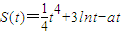，要使在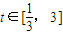上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．查看习题详情和答案>>