摘要:且.得.从而
网址:http://m.1010jiajiao.com/timu_id_390357[举报]
从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).(甲)一水池有2个进水口,1个出水口,每口进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)

给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断序号是________.
(乙)深圳市的一种特色水果上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.①f(x)p·qx;②f(x)=px2+qx+1;③f(x)=x(x-q)2+p
(以上三式中p,q均为常数,且q>1,x=0表示4月1日,x=1表示5月1日,依次类推).
(1)为准确研究其价格走势,应选________种价格模拟函数.
(2)若f(x)=4,f(2)=6,预测该果品在________月份内价格下跌.
已知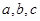 均为实数,且
均为实数,且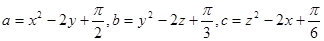 ,
,
求证: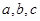 中至少有一个大于
中至少有一个大于 。
。
【解析】利用反证法的思想进行证明即可。首先否定结论假设a,b,c都不大于0然后在假设的前提下,即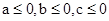 ,得
,得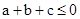 ,而
,而 ,即
,即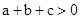 ,与
,与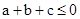 矛盾从而得到矛盾,假设不成立。
矛盾从而得到矛盾,假设不成立。
查看习题详情和答案>>
现有甲、乙两个靶,某射手进行射击训练,每次射击击中甲靶的概率是p1,每次射击击中乙靶的概率是p2,其中p1>p2,已知该射手先后向甲、乙两靶各射击一次,两次都能击中与两次都不能击中的概率分别为
,
.该射手在进行射击训练时各次射击结果互不影响.
(Ⅰ)求p1,p2的值;
(Ⅱ)假设该射手射击乙靶三次,每次射击击中目标得1分,未击中目标得0分.在三次射击中,若有两次连续击中,而另外一次未击中,则额外加1分;若三次全击中,则额外加3分.记η为该射手射击三次后的总的分数,求η的分布列;
(Ⅲ)某研究小组发现,该射手在n次射击中,击中目标的次数X服从二项分布.且射击甲靶10次最有可能击中8次,射击乙靶10次最有可能击中7次.试探究:如果X:B(n,p),其中0<p<1,求使P(X=k)(0≤k≤n)最大自然数k.
查看习题详情和答案>>
| 8 |
| 15 |
| 1 |
| 15 |
(Ⅰ)求p1,p2的值;
(Ⅱ)假设该射手射击乙靶三次,每次射击击中目标得1分,未击中目标得0分.在三次射击中,若有两次连续击中,而另外一次未击中,则额外加1分;若三次全击中,则额外加3分.记η为该射手射击三次后的总的分数,求η的分布列;
(Ⅲ)某研究小组发现,该射手在n次射击中,击中目标的次数X服从二项分布.且射击甲靶10次最有可能击中8次,射击乙靶10次最有可能击中7次.试探究:如果X:B(n,p),其中0<p<1,求使P(X=k)(0≤k≤n)最大自然数k.
一个盒子内装有八张卡片,每张卡片上面分别写着下列函数中的一个:f1(x)=x,f2(x)=2x,f3(x)=ln(|x|+3),f4(x)=sinx,f5(x)=|sinx|,f6(x)=cosx,f7(x)=cos|x|,f8(x)=3,而且不同卡片上面写着的函数互不相同,每张卡片被取出的概率相等.
(1)如果从盒子中一次随机取出两张卡片,并且将取出的两张卡片上的函数相加得到一个新函数,求所得新函数是奇函数的概率;
(2)现从盒子中一次随机取出一张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的函数是偶函数则停止取出卡片,否则继续取出卡片.设取出了ξ次才停止取出卡片,求ξ的数学期望. 查看习题详情和答案>>
(1)如果从盒子中一次随机取出两张卡片,并且将取出的两张卡片上的函数相加得到一个新函数,求所得新函数是奇函数的概率;
(2)现从盒子中一次随机取出一张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的函数是偶函数则停止取出卡片,否则继续取出卡片.设取出了ξ次才停止取出卡片,求ξ的数学期望. 查看习题详情和答案>>