摘要:(2)①由求根公式.得.
网址:http://m.1010jiajiao.com/timu_id_358229[举报]
如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么由求根公式可知,x1=
,x2=
.
于是有x1+x2=
=-
,x1•x2=
=
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
,x1x2=
这是一元二次方程根与系数的关系,我们可以利用它来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则
+
=(x1+x^)2-2x1x2=(-6)2-2×(-3)=42.
请你根据以上材料解答下列题:
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)已知x1,x2是方程x2-4x+2=0的两根,求(x1-x2)2的值. 查看习题详情和答案>>
-b+
| ||
| 2a |
-b-
| ||
| 2a |
于是有x1+x2=
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| c |
| a |
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
| b |
| a |
| c |
| a |
这是一元二次方程根与系数的关系,我们可以利用它来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则
| x | 2 1 |
| x | 2 2 |
请你根据以上材料解答下列题:
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)已知x1,x2是方程x2-4x+2=0的两根,求(x1-x2)2的值. 查看习题详情和答案>>
如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么由求根公式可知,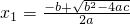 ,
,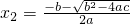 .
.
于是有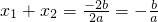 ,
,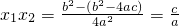
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有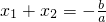 ,
,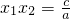
这是一元二次方程根与系数的关系,我们可以利用它来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则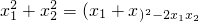 =(-6)2-2×(-3)=42.
=(-6)2-2×(-3)=42.
请你根据以上材料解答下列题:
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)已知x1,x2是方程x2-4x+2=0的两根,求(x1-x2)2的值.
查看习题详情和答案>>
如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么由求根公式可知,x1=
,x2=
.
于是有x1+x2=
=-
,x1-x2=
=
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
,x1x2=
这是一元二次方程根与系数的关系,我们可以利用它来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则
+
=(x1+x^)2-2x1x2=(-6)2-2×(-3)=42.
请你根据以上材料解答下列题:
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)已知x1,x2是方程x2-4x+2=0的两根,求(x1-x2)2的值.
查看习题详情和答案>>
-b+
| ||
| 2a |
-b-
| ||
| 2a |
于是有x1+x2=
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| c |
| a |
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-
| b |
| a |
| c |
| a |
这是一元二次方程根与系数的关系,我们可以利用它来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则
| x | 21 |
| x | 22 |
请你根据以上材料解答下列题:
(1)若x2+bx+c=0的两根为1和3,求b和c的值.
(2)已知x1,x2是方程x2-4x+2=0的两根,求(x1-x2)2的值.
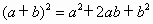 变形可得:
变形可得: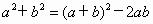 .若把此结论代入两数差的完全平方公式
.若把此结论代入两数差的完全平方公式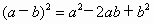 中,你能得到什么结论?根据得到的结论,你能解决下面的问题吗?
中,你能得到什么结论?根据得到的结论,你能解决下面的问题吗?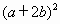 的值.
的值. ,
,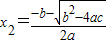 .
.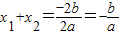 ,
,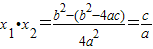
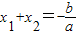 ,
,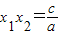
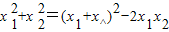 =(-6)2-2×(-3)=42.
=(-6)2-2×(-3)=42.