摘要：因为面.所以.则平面．
网址：http://m.1010jiajiao.com/timu_id_345774[举报]
如图，在四棱锥
中，
⊥底面
，底面为正方形，
，
，
分别是
，
的中点．
（I）求证：
平面
；
（II）求证：
；
（III）设PD=AD=a, 求三棱锥B-EFC的体积.
【解析】第一问利用线面平行的判定定理，
，得到
第二问中，利用
，所以
又因为
，
，从而得
第三问中，借助于等体积法来求解三棱锥B-EFC的体积.
（Ⅰ）证明：
分别是
的中点，
，． …4分
（Ⅱ）证明：四边形为正方形，．
， ．
， 
，
．，． ………8分
（Ⅲ）解：连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴
查看习题详情和答案>>
下列推理正确的是（ ）
A．因为正方形的对角线互相平分且相等，所以若一个四边形的对角线互相平分且相等，则此四边形是正方形
B．空间不共面的三条直线a，b，c，如果a⊥b，b⊥c，那么a⊥c
C．因为当x≤0，x（x-1）+1＞0；当x≥1时，x（x-1）+1＞0，所以不等式x（x-1）+1＞0在R上恒成立
D．如果a＞b，c＞d，则a-d＞b-c
查看习题详情和答案>>
A．因为正方形的对角线互相平分且相等，所以若一个四边形的对角线互相平分且相等，则此四边形是正方形
B．空间不共面的三条直线a，b，c，如果a⊥b，b⊥c，那么a⊥c
C．因为当x≤0，x（x-1）+1＞0；当x≥1时，x（x-1）+1＞0，所以不等式x（x-1）+1＞0在R上恒成立
D．如果a＞b，c＞d，则a-d＞b-c
查看习题详情和答案>>
给出以下命题：
（1）α，β表示平面，a，b，c表示直线，点M；若a?α，b?β，α∩β=c，a∩b=M，则M∈c；
（2）平面内有两个定点F1（0，3），F2（0-3）和一动点M，若||MF1|-|MF2||=2a（a＞0）是定值，则点M的轨迹是双曲线；
（3）在复数范围内分解因式：x2-3x+5=(x-
)(x-
)；
（4）抛物线y2=12x上有一点P到其焦点的距离为6，则其坐标为P（3，±6）．
以上命题中所有正确的命题序号为
查看习题详情和答案>>
（1）α，β表示平面，a，b，c表示直线，点M；若a?α，b?β，α∩β=c，a∩b=M，则M∈c；
（2）平面内有两个定点F1（0，3），F2（0-3）和一动点M，若||MF1|-|MF2||=2a（a＞0）是定值，则点M的轨迹是双曲线；
（3）在复数范围内分解因式：x2-3x+5=(x-
3+
| ||
| 2 |
3-
| ||
| 2 |
（4）抛物线y2=12x上有一点P到其焦点的距离为6，则其坐标为P（3，±6）．
以上命题中所有正确的命题序号为
（1）（3）（4）
（1）（3）（4）
．
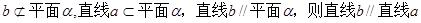”。这个结论显然是错误的，这是因为（ ）