网址:http://m.1010jiajiao.com/timu_id_345391[举报]
A.必做题部分
一、填空题:本大题共14小题,每小题5分,共70分.
1.已知全集U={1,2,3,4,5,6,7},集合/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image004.gif) ,则集合
,则集合/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image006.gif) = ▲
.
= ▲
.
2. 已知函数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image009.gif) ,则
,则/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image011.gif) 的最小正周期是 ▲ .
的最小正周期是 ▲ .
3. 经过点(-2,3),且与直线/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image013.gif) 平行的直线方程为 ▲ .
平行的直线方程为 ▲ .
4. 若复数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image015.gif) 满足
满足/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image017.gif) 则
则/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image019.gif) ▲ .
▲ .
5. 程序如下:
t←1
i←2
While i≤4
t←t×i
i←i+1
End While
Print t
以上程序输出的结果是 ▲ .
6. 若/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image021.gif) 的方差为3,则
的方差为3,则/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image023.gif) 的方差
的方差
为 ▲ .
7. 正方体ABCD-A1B/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image025.gif) ,则四面体
,则四面体/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image027.gif) 的外接球的体积为 ▲ .
的外接球的体积为 ▲ .
8. 以椭圆/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image029.gif) 的左焦点
的左焦点/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image031.gif) 为圆心,c为半径的圆与椭圆的左准线交于不同的两点,则该椭圆的离心率的取值范围是 ▲ .
为圆心,c为半径的圆与椭圆的左准线交于不同的两点,则该椭圆的离心率的取值范围是 ▲ .
9. 设a>0,集合A={(x,y)|/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image033.gif) },B={(x,y)|
},B={(x,y)|/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image035.gif) }.若点P(x,y)∈A是点P(x,y)∈B的必要不充分条件,则a的取值范围是 ▲ .
}.若点P(x,y)∈A是点P(x,y)∈B的必要不充分条件,则a的取值范围是 ▲ .
10.在闭区间 [-1,1]上任取两个实数,则它们的和不大于1的概率是 ▲ .
11.数列/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image037.gif) 中,
中,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image039.gif) ,且
,且/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image041.gif) (
(/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image043.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image045.gif) ),则这个数列的通项公式
),则这个数列的通项公式
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image047.gif) ▲
.
▲
.
12.根据下面一组等式:
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image049.gif)
…………
可得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image051.gif) ▲ .
▲ .
13.在△ABC中,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image053.gif) ,D是BC边上任意一点(D与B、C不重合),且
,D是BC边上任意一点(D与B、C不重合),且/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image055.gif) ,则
,则/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image057.gif) 等于 ▲ .
等于 ▲ .
14.设函数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image059.gif) ,记
,记/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image061.gif) ,若函数
,若函数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image063.gif) 至少存在一个零点,则实数m的取值范围是 ▲ .
至少存在一个零点,则实数m的取值范围是 ▲ .
答案:1.{6,7} 2./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image134.gif) 3.
3./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image136.gif) 4.
4./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image138.gif) 5.24 6.27 7.
5.24 6.27 7./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image140.gif) 8.
8./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image142.gif)
9.0<a≤/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image144.gif) 10.
10./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image146.gif) 11.
11./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image148.gif) 12.
12./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image150.gif) 13.
13./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image152.gif) 14.
14./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image154.gif)
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image064.gif) 二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.
二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题14分)
如图,在正三棱柱ABC-A1B
(1)求证:AD⊥平面BC C1 B1;
(2)设E是B/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image066.gif) 的值为多少时,
的值为多少时,
A1E∥平面ADC1?请给出证明.
解: (1)在正三棱柱中,C C1⊥平面ABC,AD/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image156.gif) 平面ABC,
平面ABC,
∴ AD⊥C C1.………………………………………2分
又AD⊥C1D,C C1交C1D于C1,且C C1和C1D都在面BC C1 B1内,
∴ AD⊥面BC C1 B1. ……………………………………………………………5分
(2)由(1),得AD⊥BC.在正三角形ABC中,D是BC的中点.………………………7分
当/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image158.gif) ,即E为B
,即E为B
事实上,正三棱柱ABC-A1B
又B1B∥AA1,且B1B=AA1,
∴DE∥AA1,且DE=AA1. ……………………………………………………………12分
所以四边形ADE A1为平行四边形,所以E A1∥AD.
而E A1/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image160.gif) 面AD C1内,故A1E∥平面AD C1. ………………………………………14分
面AD C1内,故A1E∥平面AD C1. ………………………………………14分
16.(本小题14分)
如图,在四边形ABCD中,AD=8,CD=6,AB=13,∠ADC=90°,且/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image068.gif) .
.
(1)求sin∠BAD的值;
(2)设△ABD的面积为S△ABD,△BCD的面积为S△BCD,求/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image070.gif) 的值.
的值.
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image071.gif) 解 (1)在Rt△ADC中,AD=8,CD=6,
解 (1)在Rt△ADC中,AD=8,CD=6,
则AC=10,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image162.gif) .………………2分
.………………2分
又∵/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image068.gif) ,AB=13,
,AB=13,
∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image165.gif) . …………………………4分
. …………………………4分
∵/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image167.gif) ,∴
,∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image169.gif) . …………………………………………………5分
. …………………………………………………5分
∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image171.gif) .……………………………………………………8分
.……………………………………………………8分
(2)/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image173.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image175.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image177.gif) , 11分
, 11分
则/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image179.gif) ,∴
,∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image181.gif) .……………………………………14分
.……………………………………14分
17.(本小题15分)
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了
日 期
温差/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image073.gif) (°C)
(°C)
10
11
13
12
8
发芽数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image075.gif) (颗)
(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image077.gif) ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
解:(1)设抽到不相邻两组数据为事件/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image183.gif) ,因为从5组数据中选取2组数据共有10种情况,每种情况都是等可能出现的,其中抽到相邻两组数据的情况有4种, ………………2分
,因为从5组数据中选取2组数据共有10种情况,每种情况都是等可能出现的,其中抽到相邻两组数据的情况有4种, ………………2分
所以 /江苏省南通市2009届高三上学期期末调研测试数学试题.files/image185.gif) .…………………………………………………………………4分
.…………………………………………………………………4分
答:略. ……………………………………………………………………………………5分
(2)由数据,求得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image187.gif) .………………………………………………………………7分
.………………………………………………………………7分
由公式,求得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image189.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image191.gif) . …………………………………………………9分
. …………………………………………………9分
所以y关于x的线性回归方程为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image193.gif) . …………………………………………10分
. …………………………………………10分
(3)当x=10时,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image195.gif) ,|22-23|<2;…………………………………………12分
,|22-23|<2;…………………………………………12分
同样,当x=8时,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image197.gif) ,|17-16|<2.……………………………………14分
,|17-16|<2.……………………………………14分
所以,该研究所得到的线性回归方程是可靠的. ……………………………………15分
18.(本小题15分)
抛物线/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image079.gif) 的焦点为F,
的焦点为F,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image081.gif) 在抛物线上,且存在实数λ,使
在抛物线上,且存在实数λ,使/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image083.gif) 0,
0,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image085.gif) .
.
(1)求直线AB的方程;
(2)求△AOB的外接圆的方程.
解:(1)抛物线/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image079.gif) 的准线方程为
的准线方程为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image199.gif) .
.
∵/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image201.gif) ,∴A,B,F三点共线.由抛物线的定义,得|
,∴A,B,F三点共线.由抛物线的定义,得|/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image203.gif) |=
|=/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image205.gif) . …1分
. …1分
设直线AB:/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image207.gif) ,而
,而/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image209.gif)
由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image211.gif) 得
得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image213.gif) . ……………………………………………3分
. ……………………………………………3分
∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image215.gif) |
|/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image203.gif) |=
|=/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image205.gif) =
= /江苏省南通市2009届高三上学期期末调研测试数学试题.files/image217.gif) .∴
.∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image219.gif) .……………6分
.……………6分
从而/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image221.gif) ,故直线AB的方程为
,故直线AB的方程为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image223.gif) ,即
,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image225.gif) .……………………8分
.……………………8分
(2)由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image227.gif) 求得A(4,4),B(
求得A(4,4),B(/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image229.gif) ,-1).……………………………………10分
,-1).……………………………………10分
设△AOB的外接圆方程为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image231.gif) ,则
,则
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image233.gif) 解得
解得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image235.gif) ………………………………………………14分
………………………………………………14分
故△AOB的外接圆的方程为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image237.gif) .…………………………………15分
.…………………………………15分
19.(本小题16分)
已知函数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image087.gif) 在[1,+∞)上为增函数,且θ∈(0,π),
在[1,+∞)上为增函数,且θ∈(0,π),/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image089.gif) ,m∈R.
,m∈R.
(1)求θ的值;
(2)若/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image091.gif) 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image093.gif) ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image095.gif) ,使得
,使得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image097.gif) 成立,求
成立,求/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image099.gif) 的取值范围.
的取值范围.
解:(1)由题意,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image239.gif) ≥0在
≥0在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image241.gif) 上恒成立,即
上恒成立,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image243.gif) .………1分
.………1分
∵θ∈(0,π),∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image245.gif) .故
.故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image247.gif) 在
在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image241.gif) 上恒成立,…………………2分
上恒成立,…………………2分
只须/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image249.gif) ,即
,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image251.gif) ,只有
,只有/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image253.gif) .结合θ∈(0,π),得
.结合θ∈(0,π),得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image255.gif) .……4分
.……4分
(2)由(1),得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image257.gif)
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image259.gif) .
./江苏省南通市2009届高三上学期期末调研测试数学试题.files/image261.gif) .…………5分
.…………5分
∵/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image091.gif) 在其定义域内为单调函数,
在其定义域内为单调函数,
∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image264.gif) 或者
或者/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image266.gif) 在[1,+∞)恒成立.………………………6分
在[1,+∞)恒成立.………………………6分
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image264.gif) 等价于
等价于/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image269.gif) ,即
,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image271.gif) ,
,
而 /江苏省南通市2009届高三上学期期末调研测试数学试题.files/image273.gif) ,(
,(/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image275.gif) )max=1,∴
)max=1,∴/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image277.gif) . …………………………………………8分
. …………………………………………8分
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image266.gif) 等价于
等价于/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image280.gif) ,即
,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image282.gif) 在[1,+∞)恒成立,
在[1,+∞)恒成立,
而/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image284.gif) ∈(0,1],
∈(0,1],/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image286.gif) .
.
综上,m的取值范围是/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image288.gif) . ………………………………………………10分
. ………………………………………………10分
(3)构造/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image290.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image292.gif) .
.
当/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image286.gif) 时,
时,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image295.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image297.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image299.gif) ,所以在[1,e]上不存在一个
,所以在[1,e]上不存在一个/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image095.gif) ,使得
,使得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image097.gif) 成立. ………………………………………………………12分
成立. ………………………………………………………12分
当/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image301.gif) 时,
时,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image303.gif) .…………………………14分
.…………………………14分
因为/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image295.gif) ,所以
,所以/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image305.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image307.gif) ,所以
,所以/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image309.gif) 在
在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image295.gif) 恒成立.
恒成立.
故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image311.gif) 在
在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image313.gif) 上单调递增,
上单调递增,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image315.gif) ,只要
,只要/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image317.gif) ,
,
解得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image319.gif) .
.
故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image099.gif) 的取值范围是
的取值范围是/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image322.gif) .………………………………………………………16分
.………………………………………………………16分
20.(本小题16分)
已知等差数列/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image101.gif) 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image103.gif) 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image105.gif) .
.
(1)求a的值;
(2)若对于任意的/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image107.gif) ,总存在
,总存在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image109.gif) ,使得
,使得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image111.gif) 成立,求b的值;
成立,求b的值;
(3)令/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image113.gif) ,问数列
,问数列/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image115.gif) 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
解:(1)由已知,得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image324.gif) .由
.由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image105.gif) ,得
,得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image327.gif) .
.
因a,b都为大于1的正整数,故a≥2.又/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image329.gif) ,故b≥3. …………………………2分
,故b≥3. …………………………2分
再由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image331.gif) ,得
,得 /江苏省南通市2009届高三上学期期末调研测试数学试题.files/image333.gif) .
.
由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image329.gif) ,故
,故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image335.gif) ,即
,即/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image337.gif) .
.
由b≥3,故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image339.gif) ,解得
,解得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image341.gif) .
………………………………………………………4分
.
………………………………………………………4分
于是/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image343.gif) ,根据
,根据/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image345.gif) ,可得
,可得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image347.gif) .…………………………………………………6分
.…………………………………………………6分
(2)由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image347.gif) ,对于任意的
,对于任意的/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image349.gif) ,均存在
,均存在/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image109.gif) ,使得
,使得/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image352.gif) ,则
,则
/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image354.gif) .
.
又/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image356.gif) ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.
故/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image358.gif) ,b=5.
,b=5.
所以b=5时,存在正自然数/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image360.gif) 满足题意.…………………………………………9分
满足题意.…………………………………………9分
(3)设数列/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image115.gif) 中,
中,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image362.gif) 成等比数列,由
成等比数列,由/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image364.gif) ,
,/江苏省南通市2009届高三上学期期末调研测试数学试题.files/image366.gif) ,得
,得

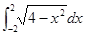 =________.[来源:学,科,网]
=________.[来源:学,科,网]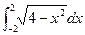 =________.[来源:学,科,网]
=________.[来源:学,科,网]