摘要:所以.若存在实数.使.则
网址:http://m.1010jiajiao.com/timu_id_336656[举报]
对于非空实数集 ,记
,记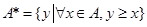 .设非空实数集合
.设非空实数集合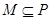 ,若
,若 时,则
时,则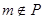 .
现给出以下命题:
.
现给出以下命题:
①对于任意给定符合题设条件的集合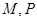 ,必有
,必有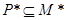 ;
;
②对于任意给定符合题设条件的集合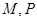 ,必有
,必有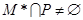 ;
;
③对于任意给定符合题设条件的集合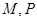 ,必有
,必有 ;
;
④对于任意给定符合题设条件的集合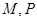 ,必存在常数
,必存在常数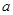 ,使得对任意的
,使得对任意的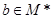 ,恒有
,恒有 ,
,
其中正确的命题是 .(写出所有正确命题的序号)
查看习题详情和答案>>
对于非空实数集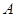 ,记
,记 .设非空实数集合
.设非空实数集合 ,若
,若 时,则
时,则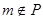 . 现给出以下命题:
. 现给出以下命题:
①对于任意给定符合题设条件的集合 ,必有
,必有 ;
;
②对于任意给定符合题设条件的集合 ,必有
,必有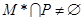 ;
;
③对于任意给定符合题设条件的集合 ,必有
,必有 ;
;
④对于任意给定符合题设条件的集合 ,必存在常数
,必存在常数 ,使得对任意的
,使得对任意的 ,恒有
,恒有 ,
,
其中正确的命题是 .(写出所有正确命题的序号)
对于非空实数集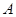 ,记
,记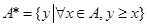 .设非空实数集合
.设非空实数集合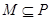 ,若
,若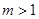 时,则
时,则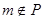 . 现给出以下命题:
. 现给出以下命题:
①对于任意给定符合题设条件的集合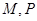 ,必有
,必有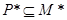 ;
;
②对于任意给定符合题设条件的集合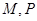 ,必有
,必有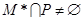 ;
;
③对于任意给定符合题设条件的集合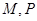 ,必有
,必有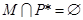 ;
;
④对于任意给定符合题设条件的集合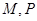 ,必存在常数
,必存在常数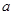 ,使得对任意的
,使得对任意的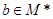 ,恒有
,恒有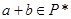 ,
,
其中正确的命题是 .(写出所有正确命题的序号)
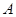 ,记
,记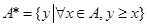 .设非空实数集合
.设非空实数集合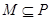 ,若
,若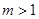 时,则
时,则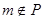 . 现给出以下命题:
. 现给出以下命题:①对于任意给定符合题设条件的集合
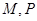 ,必有
,必有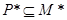 ;
;②对于任意给定符合题设条件的集合
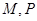 ,必有
,必有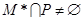 ;
;③对于任意给定符合题设条件的集合
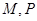 ,必有
,必有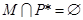 ;
; ④对于任意给定符合题设条件的集合
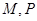 ,必存在常数
,必存在常数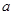 ,使得对任意的
,使得对任意的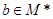 ,恒有
,恒有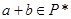 ,
,其中正确的命题是 .(写出所有正确命题的序号)
(理)定义:若存在常数k,使得对定义域D内的任意两个不同的实数x1,x2,均有:|f(x1)-f(x2)|≤k|x1-x2|成立,则称f(x)在D上满足利普希茨(Lipschitz)条件.
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数k的值,并加以验证;
(2)若函数f(x)=
在[1,+∞)上满足利普希茨(Lipschitz)条件,求常数k的最小值;
(3)现有函数f(x)=sinx,请找出所有的一次函数g(x),使得下列条件同时成立:
①函数g(x)满足利普希茨(Lipschitz)条件;
②方程g(x)=0的根t也是方程f(
)=
sin(
-
)=-
cos
=-1;
③方程f(g(x))=g(f(x))在区间[0,2π)上有且仅有一解.
查看习题详情和答案>>
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数k的值,并加以验证;
(2)若函数f(x)=
| x+1 |
(3)现有函数f(x)=sinx,请找出所有的一次函数g(x),使得下列条件同时成立:
①函数g(x)满足利普希茨(Lipschitz)条件;
②方程g(x)=0的根t也是方程f(
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
③方程f(g(x))=g(f(x))在区间[0,2π)上有且仅有一解.