摘要:又.所以是首项为.公比为的等比数列.得
网址:http://m.1010jiajiao.com/timu_id_336631[举报]
在二项式定理这节教材中有这样一个性质:![]()
(1)计算![]() 的值方法如下:
的值方法如下:
设![]() 又
又![]()
相加得![]() 即2S=5·23
即2S=5·23
所以2S=5·22=20利用类似方法求值:
![]()
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求
![]()
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
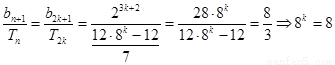
 ,
,
查看习题详情和答案>>
在二项式定理这节教材中有这样一个性质:Cn0+Cn1+Cn2+Cn3+…Cnn=2n,n∈N
(1)计算1•C30+2•C31+3•C32+4•C33的值方法如下:
设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
所以2S=5•22=20利用类似方法求值:1•C20+2•C21+3•C22,1•C40+2•C41+3•C42+4•C43+5•C44
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn,n∈N.
查看习题详情和答案>>
(1)计算1•C30+2•C31+3•C32+4•C33的值方法如下:
设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
所以2S=5•22=20利用类似方法求值:1•C20+2•C21+3•C22,1•C40+2•C41+3•C42+4•C43+5•C44
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn,n∈N.
在二项式定理这节教材中有这样一个性质:Cn0+Cn1+Cn2+Cn3+…Cnn=2n,n∈N
(1)计算1•C30+2•C31+3•C32+4•C33的值方法如下:
设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
所以2S=5•22=20利用类似方法求值:1•C20+2•C21+3•C22,1•C40+2•C41+3•C42+4•C43+5•C44
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn,n∈N.
查看习题详情和答案>>
在二项式定理这节教材中有这样一个性质:Cn0+Cn1+Cn2+Cn3+…Cnn=2n,n∈N
(1)计算1•C30+2•C31+3•C32+4•C33的值方法如下:
设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
所以2S=5•22=20利用类似方法求值:1•C20+2•C21+3•C22,1•C40+2•C41+3•C42+4•C43+5•C44
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn,n∈N.
查看习题详情和答案>>
(1)计算1•C30+2•C31+3•C32+4•C33的值方法如下:
设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
所以2S=5•22=20利用类似方法求值:1•C20+2•C21+3•C22,1•C40+2•C41+3•C42+4•C43+5•C44
(2)将(1)的情况推广到一般的结论,并给予证明
(3)设Sn是首项为a1,公比为q的等比数列{an}的前n项的和,求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn,n∈N.