摘要:所以.定义域为.
网址:http://m.1010jiajiao.com/timu_id_335891[举报]
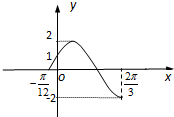 定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π | 2 |
(1)f(x)的表达式;
(2)f(x)的单调增区间;
(3)f(x)的对称轴和对称中心;
(4)f(x)的最小值以及取得最小值时的x的集合.
 定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示:
定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示:现有以下命题:
(1)方程f[g(x)]=0有且仅有三个解;
(2)方程g[f(x)]=0有且仅有三个解;
(3)方程g[g(x)]=0有且仅有一个解;
(4)方程f[f(x)]=0有且仅有九个解.
则其中正确的命题是( )
查看习题详情和答案>>
设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量
=(x1,y1),
=(x2,y2),
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=λ
+(1-λ)
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
①A、B、N三点共线;
②直线MN的方向向量可以为
=(0,1);
③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准
下线性近似”.
其中所有正确结论的番号为______.
查看习题详情和答案>>
| OA |
| OB |
| OM |
| ON |
| OA |
| OB |
| MN |
①A、B、N三点共线;
②直线MN的方向向量可以为
| a |
③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准
| 5 |
| 4 |
其中所有正确结论的番号为______.
设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量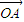 =(x1,y1),
=(x1,y1),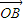 =(x2,y2),
=(x2,y2), =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量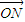 =λ
=λ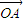 +(1-λ)
+(1-λ)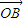 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|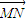 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
①A、B、N三点共线;
②直线MN的方向向量可以为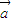 =(0,1);
=(0,1);
③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准 下线性近似”.
下线性近似”.
其中所有正确结论的番号为 . 查看习题详情和答案>>
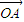 =(x1,y1),
=(x1,y1),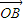 =(x2,y2),
=(x2,y2), =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量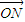 =λ
=λ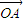 +(1-λ)
+(1-λ)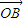 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|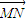 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;
②直线MN的方向向量可以为
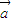 =(0,1);
=(0,1);③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准
 下线性近似”.
下线性近似”.其中所有正确结论的番号为 . 查看习题详情和答案>>
设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量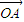 =(x1,y1),
=(x1,y1),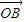 =(x2,y2),
=(x2,y2),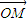 =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量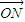 =λ
=λ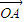 +(1-λ)
+(1-λ)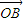 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|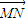 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
①A、B、N三点共线;
②直线MN的方向向量可以为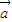 =(0,1);
=(0,1);
③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准 下线性近似”.
下线性近似”.
其中所有正确结论的番号为 . 查看习题详情和答案>>
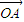 =(x1,y1),
=(x1,y1),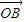 =(x2,y2),
=(x2,y2),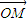 =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量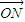 =λ
=λ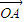 +(1-λ)
+(1-λ)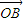 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|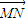 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;
②直线MN的方向向量可以为
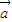 =(0,1);
=(0,1);③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准
 下线性近似”.
下线性近似”.其中所有正确结论的番号为 . 查看习题详情和答案>>