摘要：BC平面A′BC ∴平面A′BC⊥平面A′EC
网址：http://m.1010jiajiao.com/timu_id_335888[举报]
选修4－1：平面几何选讲
如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC＝ED．
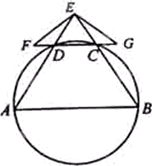
(Ⅰ)证明：CD∥AB；
(Ⅱ)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．
在四棱锥P－ABCD中，PA⊥平面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC．PA＝AB＝BC，点E在棱PB上，且PE＝2EB．
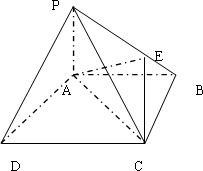
(1)求证：PD∥平面EAC；
(2)求二面角A－EC－P的余弦值的大小．
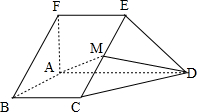如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，AF=AB=BC=FE=| 1 | 2 |
（1）求异面直线BF与DE所成的角的大小；
（2）证明平面AMD⊥平面CDE；
（3）求二面角A-CD-E的余弦值． 查看习题详情和答案>>
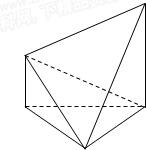如图，在多面体ABCDE中，DB⊥平面ABC，AE∥BD，且AB=BC=CA=BD=2AE=2
如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，AF=AB=BC=FE=