网址：http://m.1010jiajiao.com/timu_id_325521[举报]
一、选择题
1．C 2．C 3．A 4．B 5．A 6．D 7．B 8．A
二、填空题
9．x(x＋2)(x－2) 10．20 11．2.9×109 12．x≤2 13．18 14．70
15．7 16． 17．5 18．23
三、解答题
19．原式＝－4＋2＋1－2－＋1 …………………………4分
＝－2－． ……………………………………………8分
20．20．原式＝， ……………………………………6分
当x＝时，原式＝3（＋1）． ……………………8分
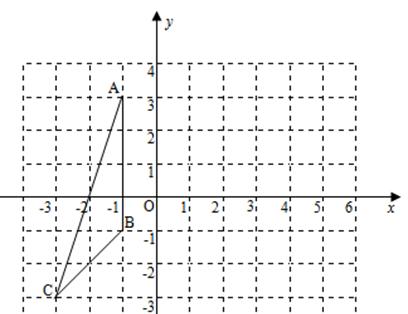
21．（1）旋转中心点P位置如图所示， ………………………2分
点P的坐标为(0，1) ………………………4分
（2）旋转后的三角形④如图所示． ………………………8分
22．(1) 100，36 ……………………………………… 4分
（2）1022 ………………………………………8分
23．（1）第一次摸的牌
第二次摸的牌
（列表略）…………………………………………………………………………（4分）
（2）P（成轴对称图形）＝ ………………………………………………（8分）
24．（1）x轴处填20，y轴处填1250；………………………………………………（4分）
（2）由图象可知，点A的坐标为（10，－2500），说明妈妈骑车速度为250米/分钟，并返回到家的时间为20分钟，设小欣早晨上学时间为x分钟，则妈妈到家后在B处追到小欣的时间为（x－20）分钟，根据题意，得：50x＝250（x－20），……………（7分）
解得：x＝25，…………………………………………………………………………（9分）
答：小欣早晨上学时间为25分钟．………………………………………………（10分）
25．AB＝×30＝20（海里）， ………………………………………………（2分）
在Rt△ABP中，BP＝＝＝40（海里），………………………………（4分）
∵∠ABP＝60°，∠CBN＝30°，
∴∠PBC＝90°…………………………………………………………………………（5分）
在Rt△BCP中，BC＝1×30＝30（海里），…………………………………………（7分）
∴PC＝＝＝50（海里）．………………………………（9分）
答：P，C之间的距离为50海里．…………………………………………………（10分）
26．（1）用直尺和圆规作图，作图痕迹清晰； ………………………………（4分）
（2）点P（1，1）关于点A（0，4）左转弯运动到P1（－3，3），……
点P1（－3，3）关于点B（－4，4）左转弯运动到点P2（－5，3），
点P2（－5，3）关于点C（－4，0）左转弯运动到点P3（－1，1），
点P3（－1，1）关于点D（0，0）左转弯运动到点P4（1，1）， ………（6分）
点P4（1，1）关于点A（0，4）左转弯运动到点P5（－3，3），
点P5与点P1重合，点P6与点P2重合，……， ………………………（8分）
点P2008的坐标为（1，1），点P2009的坐标为（－3，3），点P2010的坐标为（－5，3）． …………………………………………………………………………（10分）
27．（1）△ABP≌△BCQ，△ABE≌△BCF，△AOE≌△BOF，△BEP≌△CFQ，△ACP≌△BDQ；（从中任写出三对全等三角形）……………………………………3分
如证明△ABP≌△BCQ，
∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠BCG＝90°，…………………4分
∵BQ⊥AP，∴∠BAP＝∠CBQ， ……………………………………………………5分
∴△ABP≌△BCQ．……………………………………………………………………6分
证明其它三角形全等可参照给分．
（2）当点P为BC的中点，∠AFB＝∠CFP． ……………………………………8分
∵BP＝CP，BP＝CQ，∴CP＝CQ， ………………………………………………9分
∵AC是正方形ABCD的对角线，∴∠ACB＝∠ACD＝45°，………………………10分
∵CF＝CF，∴△CFP≌△CFQ， ……………………………………………………11分
∴∠CPF＝∠CQF，∵∠CQF＝∠APB，∴∠APB＝∠CPF． ……………………12分
证明△BEP≌△CFP可参照给分．
28．（1）令y＝0，得x2－1＝0，解得x＝±1，令x＝0，得y＝－1
∴ A（－1，0），B（1，0），C（0，－1） ……………………2分
（2）∵OA＝OB＝OC＝1 ∴∠BAC＝∠ACO＝∠BCO＝45°
∵AP∥CB， ∴∠PAB＝45°
过点P作PE⊥x轴于E，则△APE为等腰直角三角形
令OE＝a，则PE＝a＋1 ∴P（－a，a＋1）
∵点P在抛物线y＝x2－1上 ∴a＋1＝a2－1
解得a1＝2，a2＝－1（不合题意，舍去）
∴PE＝3????????????????????????????????????????????????????????????????????????????????????????????????????????????? 4分
∴四边形ACBP的面积＝AB•OC+AB•PE
＝?????????????????????????????????????????????? 6分
（3）假设存在．
∵∠PAB＝∠BAC＝45° ∴PA⊥AC
∵MGx轴于点G， ∴∠MGA＝∠PAC＝90°
在Rt△AOC中，OA＝OC＝ ∴AC＝
在Rt△PAE中，AE＝PE＝ ∴AP＝ ???????????????????????????????????????????????????????? 7分
设M点的横坐标m，则M（m，m2－1）
①点M在y轴右侧时，则m＞1
(?) 当△AMG∽△PCA时，有＝
∵AG＝m－1，MG＝m2－1
即
解得m1＝1（舍去），m2＝（舍去）
(?) 当△MAG∽△PCA时有＝
即
解得：m1＝1（舍去），m2＝2（舍去）
∴M（2，3）??????????????????????????????????????????????????????????????????????????????????????????????? 9分
② 点M在y轴左侧时，则m＜－1，
(?) 当△AMG∽△PCA时有＝
∵AG＝－m＋1，MG＝m2－1
∴
解得m1＝1（舍去），m2＝
∴M（）
(?) 当△MAG∽△PCA时有＝
即
解得： m1＝－1（舍去），m2＝－4
∴M（－4，15）
∴存在点M，使以A、M、G三点为顶点的三角形与△PCA相似
M点的坐标为（2，3），（），（－4，15）?????????????????????????????????????? 12分
（本题满分12分）已知：如图8，△ABC中，AC＝BC，以BC为直径的⊙O交AB于点D，过点D作DE⊥AC于点E，交BC的延长线于点F．（12）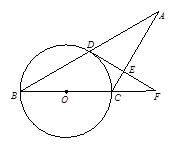
求证：（1）AD＝BD； （2）DF是⊙O的切线．
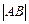。当A、B两点中有一点在原点时，不妨设点A在原点，如图(1)，
当A、B两点都不在原点时，
①如图(2)，点A、B都在原点的右边，
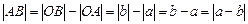；②如图(3)，点A、B都在原点的左边，
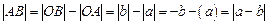；③如图(4)，点A、B都在原点的两边，
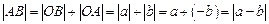；综上，数轴上A、B两点之间的距离
。
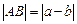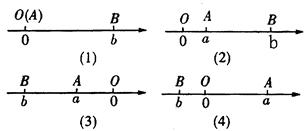
回答下列问题：
【小题1】(1)数轴上表示2和5的两点之间的距离是 ▲ ．
【小题2】(2)数轴上表示－1和－5的两点之间的距离是 ▲ ；
【小题3】(3)数轴上表示1和－4的两点之间的距离是 ▲ ；
【小题4】(4)数轴上表示x和－1的两点A之和B之间的距离是 ▲ ，如果
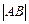＝2，那么x的值是 ▲ ．
查看习题详情和答案>>
如图，将OA = 6，AB = 4的矩形OABC放置在平面直角坐标系中，动点M、N以每秒１个单位的速度分别从点A、C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．
（1）点B的坐标为 ；用含t的式子表示点P的坐标为 ；(3分)
（2）记△OMP的面积为S，求S与t的函数关系式（0 < t < 6）；并求t为何值时，S有最大值？(4分)
（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的
？若存在，求出点T的坐标；若不存在，请说明理由．(3分)
查看习题详情和答案>>
．