（2011?郑州一模）如图所示，两平行金属板A、B长度l=0.8m，间距d=0.6m．直流电源E能提供的最大电压为9×10⁵V，位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×10⁷C/kg、重力不计的带电粒子，射人板间的粒子速度均为v₀=4×10⁶m/s．在极板右侧有一个垂直纸面向里的匀强磁场，磁感应强度B=lT，分布在环带区域中，该环带的内外圆的圆心与两板间的中心重合于O点，环带的内圆半径R_l=

2

m．将变阻器滑动头由a向b慢慢滑动，改变两板间的电压时，带电粒子均能从不同位置穿出极板射向右侧磁场，且两板间电压最大时，对应的粒子恰能从极板右侧边缘穿出． 
（1）问从板间右侧射出的粒子速度的最大值v_m是多少？
（2）若粒子射出电场时，速度的反向延长线与v₀所在直线交  于O′点，试用偏转运动相关量证明O′点与极板右端边缘的水平距离x=

1

2

，即O′与0重合，所有粒子都好像从两板的中心射 出一样． 
（3）为使粒子不从磁场右侧穿出，求环带磁场的最小宽度d．

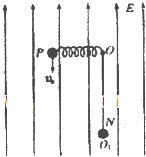（2013?南开区二模）如图所示：轻弹簧一端连于固定点O，可在竖直平面内自由转动；另一端连接一带电小球P，其质量m=2×10^-2kg，电荷量q=0.2C．将弹簧保持原长拉至水平后，以初速度v₀=20m/s竖直向下射出小球P，小球P到达O点的正下方O₁点时速度恰好水平，其大小v=15m/s．若O、O₁相距R=1.5m，小球P在点O₁与另一由细绳悬挂的、不带电的、质量M=1.6×10^-1kg的静止绝缘小球N相碰．碰后瞬间，小球P脱离弹簧，小球N脱离细绳，同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=lT的匀强磁场．此后，小球P在竖直平面内做半径r=0.5m的匀速圆周运动．小球P、N均可视为质点，小球P的电荷量保持不变，不计空气阻力，取g=10m/s²．则．
（1）判断小球P所带电性，并说明理由．
（2）弹簧从水平摆至竖直位置的过程中，其弹性势能变化了多少？
（3）请通过计算并比较相关物理量，判断小球P、N碰撞后能否在某一时刻具有相同的速度．

京广高速铁路武广段正在紧张施工，建成后将成为沟通京广的又一交通大动脉．当“和谐号”高速铁车在该高速铁路上匀速快乐地行驶时，则（　　）

（2010?重庆模拟）如图所示，光滑平行的金属导轨MN、PQ相距L=0.8m，其框架平面与水平面成．θ=30°，在M点和P点间接一个阻值为R=1.80Ω的电阻，在两一导轨间矩形区域00₁0₁′0′内有垂直导轨平面向下、宽为d=0.6m的匀强磁场，磁感应强度为B=lT．一质量为m=0.16kg、电阻为r=0.2Ω的导体棒ab，垂直搁置于导轨上，与磁场上边界相距d₀=0.4m，现使它由静止开始运动，在棒ab离开磁场前已经做匀速直线运动（棒ab与导轨始终保持良好的接触，导轨电阻不计，g=l0m/s²）求：
（1）棒ab在进人磁场上边界时的速度；
（2）棒ab在磁场中作匀速运动时产生的感应电动势；
（3）棒ab通过磁场区域过程中整个电路所产生的热量．

如图所示，一个与平台连接的足够长斜坡倾角θ=ansin

1

30

，一辆卡车的质量为l_t．关闭发动机，卡车从静止开始沿斜坡滑下，最大速度可达120km/h，已知卡车运动过程中所受空气阻力和地面阻力与速度成正比，即f=kv．
（1）求出比例系数k；
（2）现使卡车以恒定功率P沿斜坡向上行驶，达到的最大速度为54km/h，求功率P；
（3）当卡车开上平台后，继续保持此恒定功率行驶40s，重新匀速行驶，求卡车开上平台后到匀速行驶的过程中克服阻力所做的功．