摘要:得.所以.假设存在满足题意的直线.设的方程为
网址:http://m.1010jiajiao.com/timu_id_314444[举报]
已知函数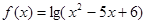 和
和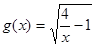 的定义域分别是集合A、B,
的定义域分别是集合A、B,
(1)求集合A,B;
(2)求集合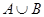 ,
,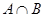 .
.
【解析】本试题考查了集合的基本运算。第一问中,利用
由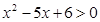 解得
解得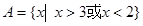
由 解得
解得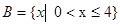
第二问中,由(1)得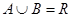
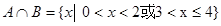
解:(1)由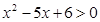 解得
解得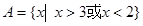 ……………………3分
……………………3分
由 解得
解得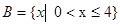 ……………………6分
……………………6分
(2)由(1)得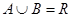 ……………………9分
……………………9分
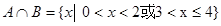
查看习题详情和答案>>
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式(1+x)2n=(1+x)n(1+x)n可得,左边xn的系数为
,而右边(1+x)n(1+x)n=(
+
x+
x2+…+
xn)(
+
x+
x2+…+
xn),xn的系数为
+
+
+…+
=(
)2+(
)2+(
)2+…+(
)2,由(1+x)2n=(1+x)n(1+x)n恒成立,可得(
)2+(
)2+(
)2+…+(
)2=
.
利用上述方法,化简(
)2-(
)2+(
)2-(
)2+…+(
)2=
查看习题详情和答案>>
| C | n 2n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | n n |
| C | 1 n |
| C | n-1 n |
| C | 2 n |
| C | n-2 n |
| C | n n |
| C | 0 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | n 2n |
利用上述方法,化简(
| C | 0 2n |
| C | 1 2n |
| C | 2 2n |
| C | 3 2n |
| C | 2n 2n |
(-1)n
| C | n 2n |
(-1)n
.| C | n 2n |
(2008•广州二模)(1)椭圆C:
+
=1(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
•
为定值b2-a2.
(2)由(1)类比可得如下真命题:双曲线C:
+
=1(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
•
为定值.请写出这个定值(不要求给出解题过程).
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| AN |
| BM |
(2)由(1)类比可得如下真命题:双曲线C:
| x2 |
| a2 |
| y2 |
| b2 |
| AN |
| BM |
对于数列{an},若存在确定的自然数T>0,使得对任意的自然数n∈N*,都有:an+T=an成立,则称数列{an}是以T为周期的周期数列.
(1)记Sn=a1+a2+a3+…+an,若{an}满足an+2=an+1-an,且S2=1007,S3=2010,求证:数列{an}是以6为周期的周期数列,并求S2009;
(2)若{an}满足a1=p∈[0,
),且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;
(3)由(1)得数列{an},又设数列{bn},其中bn=an+2n+
,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.
查看习题详情和答案>>
(1)记Sn=a1+a2+a3+…+an,若{an}满足an+2=an+1-an,且S2=1007,S3=2010,求证:数列{an}是以6为周期的周期数列,并求S2009;
(2)若{an}满足a1=p∈[0,
| 1 |
| 2 |
(3)由(1)得数列{an},又设数列{bn},其中bn=an+2n+
| 2009 |
| 2n |
 ,数列
,数列 的项满足:
的项满足: ,(1)试求
,(1)试求
 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明. ,
, 
 ,
, 
 然后再用数学归纳法分为两步骤证明即可。
然后再用数学归纳法分为两步骤证明即可。 ,
,
 ,命题成立
,命题成立 时,
时, 成立
成立 时,
时,

