摘要：(Ⅱ)求的最小值和使取得最小值的的集合.

网址：http://m.1010jiajiao.com/timu_id_304745[举报]

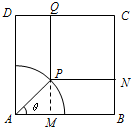精英家教网如图边长为2的正方形花园的一角是以A为中心，1为半径的扇形水池．现需在其余部分设计一个矩形草坪PNCQ，其中P是水池边上任意一点，点N、Q分别在边BC和CD上，设∠PAB为θ．
（I）用θ表示矩形草坪PNCQ的面积，并求其最小值；
（II）求点P到边BC和AB距离之比
PNPM
的最小值． 查看习题详情和答案>>
已知函数f（x）=x2+2xsinθ-1，x∈[-
3
2
，
1
2
]，θ∈[0，2π）．
（1）当θ=
π
6
时，求f（x）的最大值和最小值；
（2）求θ的范围，使f（x）在区间[-
3
2
，
1
2
]上是单调函数．
 查看习题详情和答案>>
为了研究某种药物，用小白鼠进行试验，发现药物在血液内的浓度与时间的关系因使用方式的不同而不同．若使用注射方式给药，则在注射后的3小时内，药物在白鼠血液内的浓度y1与时间t满足关系式：y1=4-at(0＜a＜
4
3
，a为常数)，若使用口服方式给药，则药物在白鼠血液内的浓度y2与时间t满足关系式：y2=
t
(0＜t＜1)
3-
2
t
(1≤t≤3)
．现对小白鼠同时进行注射和口服该种药物，且注射药物和口服药物的吸收与代谢互不干扰．
（1）若a=1，求3小时内，该小白鼠何时血液中药物的浓度最高，并求出最大值
（2）若使小白鼠在用药后3小时内血液中的药物浓度不低于4，求正数a的取值范围． 查看习题详情和答案>>
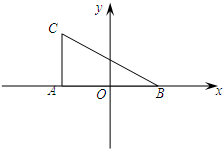精英家教网如图，在Rt△ABC中，∠CAB=90°，|AB|=2，|AC|=
3
2
，点A，B关于y轴对称．一曲线E过C点，动点P在曲线E上运动，且保持|PA|+|PB|的值不变．
（1）求曲线E的方程；
（2）已知点S(0，-
3
)，T(0，
3
)，求∠SPT的最小值；
（3）若点F(1，
3
2
)是曲线E上的一点，设M，N是曲线E上不同的两点，直线FM和FN的倾斜角互补，试判断直线MN的斜率是否为定值，如果是，求出这个定值；如果不是，请说明理由． 查看习题详情和答案>>
（2006•朝阳区二模）设对于任意实数x、y，函数f（x）、g（x）满足f（x+1）=
1
3
f（x），且f（0）=3，g（x+y）=g（x）+2y，g（5）=13，n∈N*．
（Ⅰ）求数列{f（n）}、{g（n）}的通项公式；
（Ⅱ）设cn=g[
n
2
f(n)]，求数列{cn}的前n项和Sn；
（Ⅲ）已知
lim
n
 
∞
2n+3
3n-1
=0，设F（n）=Sn-3n，是否存在整数m和M，使得对任意正整数n不等式m＜F（n）＜M恒成立？若存在，分别求出m和M的集合，并求出M-m的最小值；若不存在，请说明理由．
 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网