摘要：(2)求数列的前n项和,
网址：http://m.1010jiajiao.com/timu_id_303338[举报]
一、选择题：
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
A
D
C
A
D
C
B
D
B
C
二、填空题：
13、
14、
15、
等； 16、7
三、解答题
17、（1）由余弦定理：
又
∴
∴
（2）∵A+B+C=
∴
∴
18、（1）
（2）
19、（1）AC=1，BC=2 ，AB=
，∴
∴AC
又 平面PAC
平面ABC，平面PAC
平面ABC=AC，∴BC平面PAC
又∵PA
平面APC ∴
（2）该几何体的主试图如下：
几何体主试图的面积为
∴
∴
（3）取PC 的中点N，连接AN，由△PAC是边长为1的正三角形，可知
由（1）BC平面PAC，可知
∴
平面PCBM
∴
20、（1）
的最小值为
（2）a的取值范围是
21、（1）曲线C的方程为
（2）
，存在点M（―1，2）满足题意
22、（1）由于点B1（1，y1），B2（2，y2），…，Bn（n，yn）（
）在直线
上
则
因此
，所以
是等差数列
（2）由已知有
得
同理 
∴
∴
∴
（3）由（2）得
，则
∴
∴
∴
由于
而
则
，从而
同理：
…… 
以上
个不等式相加得：
即
，从而
（2012•卢湾区一模）已知数列{bn}，若存在正整数T，对一切n∈N*都有bn+r=bn，则称数列{bn}为周期数列，T是它的一个周期．例如：
数列a，a，a，a，…①可看作周期为1的数列；
数列a，b，a，b，…②可看作周期为2的数列；
数列a，b，c，a，b，c，…③可看作周期为3的数列…
（1）对于数列②，它的一个通项公式可以是an =
，试再写出该数列的一个通项公式；
（2）求数列③的前n项和Sn；
（3）在数列③中，若a=2，b=
，c=-1，且它有一个形如bn=Asin（ωn+φ）+B的通项公式，其中A、B、ω、φ均为实数，A＞0，ω＞0，|φ|＜
，求该数列的一个通项公式bn．
查看习题详情和答案>>
数列a，a，a，a，…①可看作周期为1的数列；
数列a，b，a，b，…②可看作周期为2的数列；
数列a，b，c，a，b，c，…③可看作周期为3的数列…
（1）对于数列②，它的一个通项公式可以是an =
|
（2）求数列③的前n项和Sn；
（3）在数列③中，若a=2，b=
| 1 |
| 2 |
| π |
| 2 |
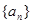和等比数列
，
，
，
，
；
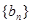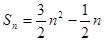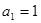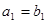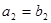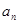和等比数列
；
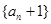的前n项和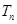
与等比数列
。
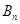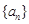中，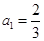
，
，
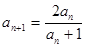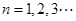
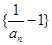是等比数列； （2）求数列
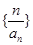的前n项和。
的前
项和
，数列
满足：
. 
的前n项和
； 
的最小值.