摘要:由三垂线定理可知
网址:http://m.1010jiajiao.com/timu_id_281964[举报]
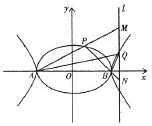 已知A,B分别是椭圆C1:
已知A,B分别是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(I)若P(
| ||
| 2 |
| 3 |
| 5 |
| 2 |
(Ⅱ)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1•k2+k3•k4为定值;
(Ⅲ)过Q作垂直于x轴的直线l,直线AP,BP分别交 l于M,N,判断△PMN是否可能为正三角形,并说明理由.
已知A,B分别是椭圆C1: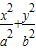 =1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2: =1上异与A,B的任意一点,a>b>0.
=1上异与A,B的任意一点,a>b>0.
(I)若P(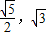 ),Q(
),Q( ,1),求椭圆Cl的方程;
,1),求椭圆Cl的方程;
(Ⅱ)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1•k2+k3•k4为定值;
(Ⅲ)过Q作垂直于x轴的直线l,直线AP,BP分别交 l于M,N,判断△PMN是否可能为正三角形,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
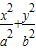 =1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2: =1上异与A,B的任意一点,a>b>0.
=1上异与A,B的任意一点,a>b>0.(I)若P(
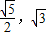 ),Q(
),Q( ,1),求椭圆Cl的方程;
,1),求椭圆Cl的方程;(Ⅱ)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1•k2+k3•k4为定值;
(Ⅲ)过Q作垂直于x轴的直线l,直线AP,BP分别交 l于M,N,判断△PMN是否可能为正三角形,并说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质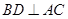 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

查看习题详情和答案>>

