摘要：故.．
网址：http://m.1010jiajiao.com/timu_id_279946[举报]
．（本小题满分12分）一位客人去北京旅游，他游览长城、故宫、鸟巢这三个景点的概率分别为０.9、0.8、0.8，且他是否游览哪个景点互不影响．设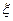
表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值．
（１）求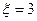
时的概率；
（２）记“函数
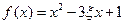在区间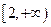
上是增函数”为事件Ａ，求事件Ａ的概率．
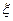表示客人离开北京时游览的景点数与没有游览的景点数之差的绝对值．（１）求
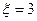时的概率；（２）记“函数
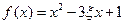在区间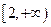上是增函数”为事件Ａ，求事件Ａ的概率．
如图，在正三棱柱ABC-A1B1C1中，E∈BB1，截面A1EC⊥侧面AC1．
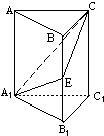
（1）求证：BE=EB1；
（2）若AA1=A1B1；求平面A1EC与平面A1B1C1所成二面角（锐角）的度数．
注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．
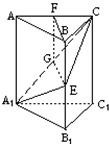
（1）证明：在截面A1EC内，过E作EG⊥A1C，G是垂足．
①∵
∴EG⊥侧面AC1；取AC的中点F，连接BF，FG，由AB=BC得BF⊥AC，
②∵
∴BF⊥侧面AC1；得BF∥EG，BF、EG确定一个平面，交侧面AC1于FG．
③∵
∴BE∥FG，四边形BEGF是平行四边形，BE=FG，
④∵
∴FG∥AA1，△AA1C∽△FGC，
⑤∵
∴FG=
AA1=
BB1，即BE=
BB1，故BE=EB1．
查看习题详情和答案>>
（1）求证：BE=EB1；
（2）若AA1=A1B1；求平面A1EC与平面A1B1C1所成二面角（锐角）的度数．
注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．
（1）证明：在截面A1EC内，过E作EG⊥A1C，G是垂足．
①∵
∴EG⊥侧面AC1；取AC的中点F，连接BF，FG，由AB=BC得BF⊥AC，
②∵
∴BF⊥侧面AC1；得BF∥EG，BF、EG确定一个平面，交侧面AC1于FG．
③∵
∴BE∥FG，四边形BEGF是平行四边形，BE=FG，
④∵
∴FG∥AA1，△AA1C∽△FGC，
⑤∵
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
深夜，一辆出租车牵涉到一起交通事故中，该市有红色与绿色两种颜色的出租车2000辆，其中绿色出租车和红色出租车分别占整个城市的85%和15%，根据现场目击者说：事故现场的出租车是红色的．有关部门对证人的辨别能力作了测试，测得他辨认的正确率为80%，于是警察就认定红色出租车有较大的肇事嫌疑．
（1）根据现场目击者的说法，填写下列的信息表，并求红色出租车肇事的概率；
（2）试问：肇事的认定对红色出租车公平吗？请说明理由．
查看习题详情和答案>>
（1）根据现场目击者的说法，填写下列的信息表，并求红色出租车肇事的概率；
| 证人所说的颜色（正确率80%） | |||
| 真实颜色 | 绿色（辆） | 红色（辆） | 合计 |
| 绿色（85%） | 1700 | ||
| 红色（15%） | 300 | ||
| 合计（辆） | 2000 | ||
如图，A处建有一个补给站，在A正西120海里处有一个港口B，一艘科考船从B出发，沿北偏东30°的方向，以20海里/小时的速度驶离港口．同时一艘为科考船运送补给的快艇从A出发，沿北偏西30°的方向，以60海里/小时的速度行驶，1小时后补给船行驶至C处，发生故障停留了1小时．快艇为在最短时间内将补给送到科考船，在C处调整航向后继续以60海里/小时的速度直线行驶，恰好与科考船在D处相遇，求相遇时科考船共行驶了多少小时．“肇实，正名芡实，因肇庆所产之芡实颗粒大、药力强，故名。”某科研所为进一步改良肇实，为此对肇实的两个品种（分别称为品种A和品种B）进行试验．选取两大片水塘，每大片水塘分成n小片水塘，在总共2n小片水塘中，随机选n小片水塘种植品种A，另外n小片水塘种植B．
（1）假设n=4，在第一大片水塘中，种植品种A的小片水塘的数目记为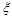
，求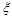的分布列和数学期望；
（2）试验时每大片水塘分成8小片，即n=8，试验结束后得到品种A和品种B在每个小片水塘上的每亩产量（单位：kg/亩）如下表：
|
号码 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
品种A |
101 |
97 |
92 |
103 |
91 |
100 |
110 |
106 |
|
品种B |
115 |
107 |
112 |
108 |
111 |
120 |
110 |
113 |
分别求品种A和品种B的每亩产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
查看习题详情和答案>>