摘要：∴的递增区间为.及.递减区间为．
网址：http://m.1010jiajiao.com/timu_id_269788[举报]
已知函数
图象的对称中心为（0,1）；函数
在 区间[－2，1）上单调递减，在[1, ＋∞）上单调递增．
（Ⅰ）求实数b的值；
（Ⅱ）求
的值及
的解析式；
（Ⅲ）设
，试证：对任意的x1、x2∈（1，＋∞）且x1≠x2，都有
．
已知函数f（x）=x3+bx2+（b2-1）x+1图象的对称中心为（0，1）；函数g(x)=ax3+
sinθ•x2-2x在 区间[-2，1）上单调递减，在[1，+∞）上单调递增．
（Ⅰ）求实数b的值；
（Ⅱ）求sinθ的值及g（x）的解析式；
（Ⅲ）设φ（x）=f（x）-g（x），试证：对任意的x1、x2∈（1，+∞）且x1≠x2，都有|φ（x2）-φ（x1）|＞2|x2-x1|． 查看习题详情和答案>>
| 1 | 2 |
（Ⅰ）求实数b的值；
（Ⅱ）求sinθ的值及g（x）的解析式；
（Ⅲ）设φ（x）=f（x）-g（x），试证：对任意的x1、x2∈（1，+∞）且x1≠x2，都有|φ（x2）-φ（x1）|＞2|x2-x1|． 查看习题详情和答案>>
已知函数f（x）=x3+bx2+（b2-1）x+1图象的对称中心为（0，1）；函数
在 区间[-2，1）上单调递减，在[1，+∞）上单调递增．
（Ⅰ）求实数b的值；
（Ⅱ）求sinθ的值及g（x）的解析式；
（Ⅲ）设φ（x）=f（x）-g（x），试证：对任意的x1、x2∈（1，+∞）且x1≠x2，都有|φ（x2）-φ（x1）|＞2|x2-x1|．
查看习题详情和答案>>
在 区间[-2，1）上单调递减，在[1，+∞）上单调递增．（Ⅰ）求实数b的值；
（Ⅱ）求sinθ的值及g（x）的解析式；
（Ⅲ）设φ（x）=f（x）-g（x），试证：对任意的x1、x2∈（1，+∞）且x1≠x2，都有|φ（x2）-φ（x1）|＞2|x2-x1|．
查看习题详情和答案>>
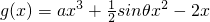在 区间[-2，1）上单调递减，在[1，+∞）上单调递增．