摘要:∴m>5,存在最小正整数m=6,使对任意n∈N*有bn<成立
网址:http://m.1010jiajiao.com/timu_id_259165[举报]
已知函数f(x)=
(x>0).
(1)求数列{an}满足a1=1,
=f(an),求an;
(2)若bn=an+12+an+22+…+a2n+12,是否存在最小正整数P,使对任意x∈N*,都有bn<
成立.
查看习题详情和答案>>
| ||
| x |
(1)求数列{an}满足a1=1,
| 1 |
| an+1 |
(2)若bn=an+12+an+22+…+a2n+12,是否存在最小正整数P,使对任意x∈N*,都有bn<
| P |
| 25 |
已知函数f(x)=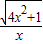 (x>0).
(x>0).
(1)求数列{an}满足a1=1,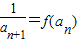 ,求an;
,求an;
(2)若bn=an+12+an+22+…+a2n+12,是否存在最小正整数P,使对任意x∈N*,都有bn<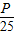 成立.
成立.
查看习题详情和答案>>
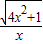 (x>0).
(x>0).(1)求数列{an}满足a1=1,
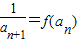 ,求an;
,求an;(2)若bn=an+12+an+22+…+a2n+12,是否存在最小正整数P,使对任意x∈N*,都有bn<
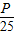 成立.
成立.查看习题详情和答案>>
设各项为正数的等比数列{an}的前n项和为Sn,S4=1,S8=17.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在最小正整数m,使得当n>m时,an<
恒成立?若存在,求出m;若不存在,请说明理由.
查看习题详情和答案>>
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在最小正整数m,使得当n>m时,an<
| 2011 | 15 |
(2012•成都一模)已知函数f(x)在[a,b]上连续,定义
;其中f(x)min(x∈D)表示f(x)在D上的最小值,f(x)max(x∈D)表示f(x)在D上的最大值.若存在最小正整数k使得f2(x)-f1(x)≤k(x-a)对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”.有下列命题:
①若f(x)=cosx,x∈[0,π],则f1(x)=1,x∈[0,π];
②若f(x)=2x,x∈[-1,4],则f2(x)=2x,x∈[-1,4]
③f(x)=x为[1,2]上的1阶收缩函数;
④f(x)=x2为[1,4]上的5阶收缩函数.
其中你认为正确的所有命题的序号为
查看习题详情和答案>>
|
①若f(x)=cosx,x∈[0,π],则f1(x)=1,x∈[0,π];
②若f(x)=2x,x∈[-1,4],则f2(x)=2x,x∈[-1,4]
③f(x)=x为[1,2]上的1阶收缩函数;
④f(x)=x2为[1,4]上的5阶收缩函数.
其中你认为正确的所有命题的序号为
②③④
②③④
.