摘要:所以为定值.其值为0. ----13分 解法二:
网址:http://m.1010jiajiao.com/timu_id_251029[举报]
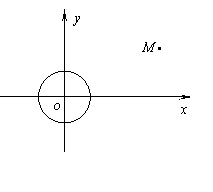 已知⊙
已知⊙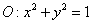 和点
和点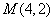 .
.
(Ⅰ)过点 向⊙
向⊙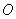 引切线
引切线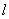 ,求直线
,求直线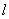 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线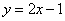 截得的弦长为 4的⊙
截得的弦长为 4的⊙ 的方程;
的方程;
(Ⅲ)设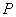 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点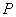 向⊙
向⊙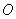 引切线,切点为Q. 试探究:平面内是否存在一定点
引切线,切点为Q. 试探究:平面内是否存在一定点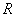 ,使得
,使得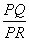 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
查看习题详情和答案>>
某制造商制造并出售球形瓶装的某种饮料,瓶子的制造成本与瓶子的半径r的平方成正比,且r=1cm时,制造成本为0.8π分.已知每出售1ml的饮料,制造商可获利0.2分,且制造商制作的瓶子的最大半径为6cm,设每瓶饮料的利润为y分,(半径r的单位是cm).
(1)写出出售每瓶饮料可得利润的关系式;
(2)求制造商制造并出售100瓶该饮料所获得的最大利润(结果用含π的式子表示).
查看习题详情和答案>>
(1)写出出售每瓶饮料可得利润的关系式;
(2)求制造商制造并出售100瓶该饮料所获得的最大利润(结果用含π的式子表示).
(2005•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为arccos
,周长为定值p,求面积S的最大值;
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:S=
absinC≤
×9×8sinC=36sinC,要使S的值最大,则应使sinC最大,即使∠C最大,也就是使∠C所对的边c边长最大,所以,当a?9,b?8,c?4时该三角形面积最大,此时cosC=
,sinC=
,所以,该三角形面积的最大值是
.以上解答是否正确?若不正确,请你给出正确的解答.
查看习题详情和答案>>
(2)若三角形有一个内角为arccos
| 7 |
| 9 |
(3)为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:S=
| 1 |
| 2 |
| 1 |
| 2 |
| 43 |
| 48 |
| ||
| 48 |
3
| ||
| 4 |
(2007•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为arccos
,周长为定值p,求面积S的最大值;
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)2-c2][c2-(a-b)2]=-c4+2(a2+b2)c2-(a2-b2)2=-[c2-(a2+b2)]2+4a2b2
而-[c2-(a2+b2)]2≤0,a2≤81,b2≤64,则S≤36,但是,其中等号成立的条件是c2=a2+b2,a=9,b=8,于是c2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
查看习题详情和答案>>
(2)若三角形有一个内角为arccos
| 7 | 9 |
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)2-c2][c2-(a-b)2]=-c4+2(a2+b2)c2-(a2-b2)2=-[c2-(a2+b2)]2+4a2b2
而-[c2-(a2+b2)]2≤0,a2≤81,b2≤64,则S≤36,但是,其中等号成立的条件是c2=a2+b2,a=9,b=8,于是c2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)