摘要:因为抛物线焦点到准线距离等于4 所以圆心的轨迹是(II)解法一:
网址:http://m.1010jiajiao.com/timu_id_251020[举报]
下列说法中,正确的有 .
①若点P(x0,y0)是抛物线y2=2px上一点,则该点到抛物线的焦点的距离是|PF|=x0+
;
②设F1、F2为双曲线
-
=1的两个焦点,P(x0,y0)为双曲线上一动点,∠F1PF2=θ,则△PF1F2的面积为b2tan
;
③设定圆O上有一动点A,圆O内一定点M,AM的垂直平分线与半径OA的交点为点P,则P的轨迹为一椭圆;
④设抛物线焦点到准线的距离为p,过抛物线焦点F的直线交抛物线于A、B两点,则
、
、
成等差数列.
查看习题详情和答案>>
①若点P(x0,y0)是抛物线y2=2px上一点,则该点到抛物线的焦点的距离是|PF|=x0+
| p |
| 2 |
②设F1、F2为双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
③设定圆O上有一动点A,圆O内一定点M,AM的垂直平分线与半径OA的交点为点P,则P的轨迹为一椭圆;
④设抛物线焦点到准线的距离为p,过抛物线焦点F的直线交抛物线于A、B两点,则
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
下列说法中,正确的有 .
①若点 是抛物线
是抛物线 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是 ;
;
②设 、
、 为双曲线
为双曲线 的两个焦点,
的两个焦点, 为双曲线上一动点,
为双曲线上一动点, ,则
,则 的面积为
的面积为 ;
;
③设定圆 上有一动点
上有一动点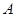 ,圆
,圆 内一定点
内一定点 ,
, 的垂直平分线与半径
的垂直平分线与半径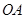 的交点为点
的交点为点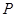 ,则
,则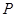 的轨迹为一椭圆;
的轨迹为一椭圆;
④设抛物线焦点到准线的距离为 ,过抛物线焦点
,过抛物线焦点 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则 、
、 、
、 成等差数列.
成等差数列.
查看习题详情和答案>>
(本小题满分12分)
已知抛物线y2=mx的焦点到准线距离为1,且抛物线开口向右.
(Ⅰ)求m的值;
(Ⅱ)P是抛物线y2=mx上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于
△PBC,求△PBC面积的最小值.
查看习题详情和答案>>
极坐标方程ρ=
所表示的曲线是( )
| 4 |
| 3-5cosθ |
A、焦点到准线距离为
| ||
B、焦点到准线距离为
| ||
C、焦点到准线距离为
| ||
D、焦点到准线距离为
|