摘要：∴k?kAN=k?=-1.∴m=.
网址：http://m.1010jiajiao.com/timu_id_248770[举报]
（2013•淄博二模）等比数列{cn}满足cn+1+cn=10•4n-1(n∈N*)，数列{an}的前n项和为Sn，且an=log2cn．
（I）求an，Sn；
（II）数列{bn}满足bn=
，Tn为数列{bn}的前n项和，是否存在正整数m，k（1＜m＜k），使得T1，Tm，Tk成等比数列？若存在，求出所有m，k的值；若不存在，请说明理由．
查看习题详情和答案>>
（I）求an，Sn；
（II）数列{bn}满足bn=
| 1 | 4Sn-1 |
已知椭圆
内一定点M(m，0)(m≠0)和直线
：
，直线与
轴交点为K．
(1)过M的任意直线与椭圆交于A、B两点，证明：∠AKM=∠BKM；
(2)过点K的直线与椭圆相交于A、E两点，设
，过点E且平行于直线的直线与椭圆相交于另一点B，证明：
．
等比数列{cn}满足
的前n项和为Sn，且an=log2cn．
（I）求an，Sn；
（II）数列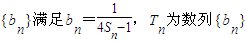
的前n项和，是否存在正整数m，k（1＜m＜k），使得T1，Tm，Tk成等比数列？若存在，求出所有m，k的值；若不存在，请说明理由．
查看习题详情和答案>>
的前n项和为Sn，且an=log2cn．（I）求an，Sn；
（II）数列
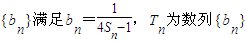的前n项和，是否存在正整数m，k（1＜m＜k），使得T1，Tm，Tk成等比数列？若存在，求出所有m，k的值；若不存在，请说明理由．查看习题详情和答案>>
在△ABC中，角A、B、C的对边分别为a、b、c，向量
=（sinA,b+c），
=（a－c,sinC－sinB）,满足
=
（Ⅰ）求角B的大小；
（Ⅱ）设
=（sin（C+
）,
）, 
=（2k,cos2A） （k>1）, 
有最大值为3，求k的值.
【解析】本试题主要考查了向量的数量积和三角函数，以及解三角形的综合运用
第一问中由条件|p +q |=| p －q |，两边平方得p·q＝0，又
p=（sinA,b+c）,q=（a－c,sinC－sinB）,代入得（a－c）sinA＋（b+c）（sinC－sinB）＝0，
根据正弦定理，可化为a（a－c）+（b+c）（c－b）=0,
即
，又由余弦定理
＝2acosB,所以cosB＝，B＝
第二问中，m=（sin（C+）,）,n=（2k,cos2A） （k>1）,m·n=2ksin（C+）+cos2A=2ksin（C+B） +cos2A
=2ksinA+
-=-
+2ksinA+=-
+ （k>1）.
而0<A<
,sinA∈（0,1],故当sin＝1时，m·n取最大值为2k-=3,得k＝
.
查看习题详情和答案>>
（2011•东城区模拟）对数列{an}，规定{△an}为数列{an}的一阶差分数列，其中△an=an+1-an（n∈N*）．对正整数k，规定 {△kan}为{an}的k阶差分数列，其中△kan=△k-1an+1-△k-1an=△（△k-1an）．
（Ⅰ）若数列{an}的首项a1=1，且满足△2an-△an+1+an=-2n，求数列{an}的通项公式；
（Ⅱ）对（Ⅰ）中的数列{an}，若数列{bn}是等差数列，使得b1Cn1+b2Cn2+b3Cn3+…+bn-1Cnn-1+bnCnn=an对一切正整数n∈N*都成立，求bn；
（Ⅲ） 在（Ⅱ）的条件下，令cn=（2n-1）bn，设Tn=
+
+
+…+
，若Tn＜m成立，求最小正整数m的值．
查看习题详情和答案>>
（Ⅰ）若数列{an}的首项a1=1，且满足△2an-△an+1+an=-2n，求数列{an}的通项公式；
（Ⅱ）对（Ⅰ）中的数列{an}，若数列{bn}是等差数列，使得b1Cn1+b2Cn2+b3Cn3+…+bn-1Cnn-1+bnCnn=an对一切正整数n∈N*都成立，求bn；
（Ⅲ） 在（Ⅱ）的条件下，令cn=（2n-1）bn，设Tn=
| c1 |
| a1 |
| c2 |
| a2 |
| c3 |
| a3 |
| cn |
| an |