摘要:成立.即(Ⅲ)的结论成立.在一般的“消元 方法中.本题三个小题中不等关系的证明过程差异较大.尤其是.许多尖子学生证明了(Ⅱ)的结论而不能解决(Ⅲ).
网址:http://m.1010jiajiao.com/timu_id_198688[举报]
某学生对函数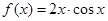 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数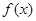 在
在 上单调递增,在
上单调递增,在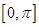 上单调递减;
上单调递减;
②点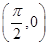 是函数
是函数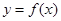 图像的一个对称中心;
图像的一个对称中心;
③函数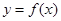 图像关于直线
图像关于直线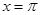 对称;
对称;
④存在常数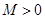 ,使
,使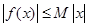 对一切实数
对一切实数 均成立.其中正确的结论是
.
均成立.其中正确的结论是
.
查看习题详情和答案>>
某学生对函数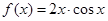 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数 在
在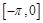 上单调递增,在
上单调递增,在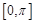 上单调递减;
上单调递减;
②点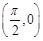 是函数
是函数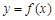 图像的一个对称中心;
图像的一个对称中心;
③函数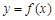 图像关于直线
图像关于直线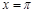 对称;
对称;
④存在常数 ,使
,使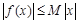 对一切实数
对一切实数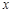 均成立.
均成立.
其中正确的结论是 .
查看习题详情和答案>>
某学生对函数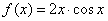 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①函数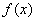 在
在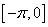 上单调递增,在
上单调递增,在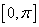 上单调递减;
上单调递减;
②点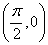 是函数
是函数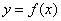 图像的一个对称中心;
图像的一个对称中心;
③函数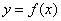 图像关于直线
图像关于直线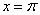 对称;
对称;
④存在常数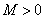 ,使
,使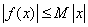 对一切实数
对一切实数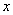 均成立.其中正确的结论是 .
均成立.其中正确的结论是 .
查看习题详情和答案>>
某港口的水深 (米)是时间
(米)是时间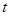 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【解析】第一问由表中数据可以看到:水深最大值为13,最小值为7,,
∴A+b=13, -A+b=7 解得 A=3, b=10
第二问要想船舶安全,必须深度 ,即
,即
∴

解得:
 得到结论。
得到结论。
查看习题详情和答案>>