网址:http://m.1010jiajiao.com/timu_id_193218[举报]
设函数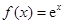 ,其中
,其中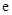 为自然对数的底数.
为自然对数的底数.
(1)求函数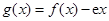 的单调区间;
的单调区间;
(2)记曲线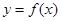 在点
在点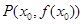 (其中
(其中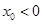 )处的切线为
)处的切线为 ,
, 与
与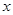 轴、
轴、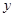 轴所围成的三角形面积为
轴所围成的三角形面积为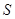 ,求
,求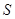 的最大值.
的最大值.
【解析】第一问利用由已知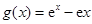 ,所以
,所以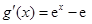 ,
,
由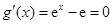 ,得
,得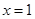 ,
所以,在区间
,
所以,在区间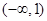 上,
上,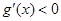 ,函数
,函数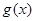 在区间
在区间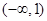 上单调递减;
在区间
上单调递减;
在区间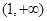 上,
上, ,函数
,函数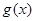 在区间
在区间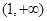 上单调递增;
上单调递增;
第二问中,因为 ,所以曲线
,所以曲线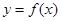 在点
在点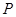 处切线为
处切线为 :
: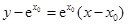 .
.
切线 与
与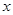 轴的交点为
轴的交点为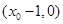 ,与
,与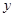 轴的交点为
轴的交点为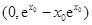 ,
,
因为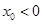 ,所以
,所以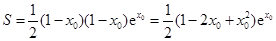 ,
,
 , 在区间
, 在区间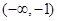 上,函数
上,函数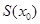 单调递增,在区间
单调递增,在区间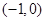 上,函数
上,函数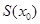 单调递减.所以,当
单调递减.所以,当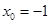 时,
时,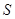 有最大值,此时
有最大值,此时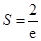 ,
,
解:(Ⅰ)由已知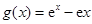 ,所以
,所以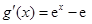 ,
由
,
由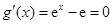 ,得
,得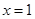 , 所以,在区间
, 所以,在区间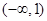 上,
上,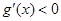 ,函数
,函数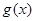 在区间
在区间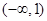 上单调递减;
上单调递减;
在区间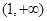 上,
上, ,函数
,函数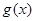 在区间
在区间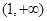 上单调递增;
上单调递增;
即函数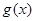 的单调递减区间为
的单调递减区间为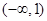 ,单调递增区间为
,单调递增区间为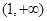 .
.
(Ⅱ)因为 ,所以曲线
,所以曲线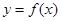 在点
在点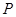 处切线为
处切线为 :
: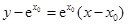 .
.
切线 与
与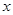 轴的交点为
轴的交点为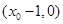 ,与
,与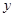 轴的交点为
轴的交点为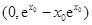 ,
,
因为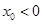 ,所以
,所以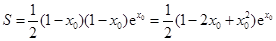 ,
,
 , 在区间
, 在区间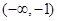 上,函数
上,函数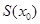 单调递增,在区间
单调递增,在区间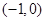 上,函数
上,函数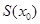 单调递减.所以,当
单调递减.所以,当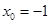 时,
时,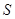 有最大值,此时
有最大值,此时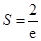 ,
,
所以,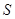 的最大值为
的最大值为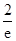
查看习题详情和答案>>
 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下: 
(1)当x>0时,
 在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______;
在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______;(2)由此可推断,当x<0时,
 有最______值为______,此时x=______;
有最______值为______,此时x=______; (3)证明:函数
 在区间(0,2)上递减;
在区间(0,2)上递减;(4)若方程x2-mx+4=0在[0,3]内有两个不相等的实数根,求实数m的取值范围。
已知函数 ,(
,( ),
),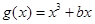
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令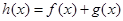 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,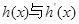 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当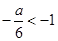 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
查看习题详情和答案>>
设函数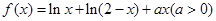 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
查看习题详情和答案>>
已知函数 ,
, .
.
(Ⅰ)若函数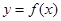 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
【解析】第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式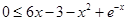 在
在 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为 ,有
,有 .
.
故 在区间
在区间 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又 [来源:]
[来源:]

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>



