网址:http://m.1010jiajiao.com/timu_id_192958[举报]
若函数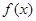 在定义域内存在区间
在定义域内存在区间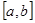 ,满足
,满足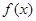 在
在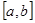 上的值域为
上的值域为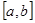 ,则称这样的函数
,则称这样的函数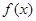 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数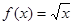 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出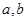 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数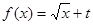 为“优美函数”,求实数
为“优美函数”,求实数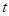 的取值范围.
的取值范围.
【解析】第一问中,利用定义,判定由题意得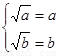 ,由
,由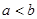 ,所以
,所以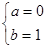
第二问中, 由题意得方程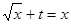 有两实根
有两实根
设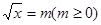 所以关于m的方程
所以关于m的方程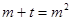 在
在 有两实根,
有两实根,
即函数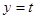 与函数
与函数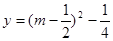 的图像在
的图像在 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。
解(I)由题意得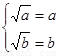 ,由
,由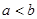 ,所以
,所以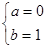 (6分)
(6分)
(II)由题意得方程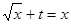 有两实根
有两实根
设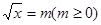 所以关于m的方程
所以关于m的方程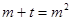 在
在 有两实根,
有两实根,
即函数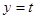 与函数
与函数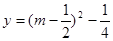 的图像在
的图像在 上有两个不同交点。
上有两个不同交点。
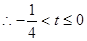
查看习题详情和答案>>
已知函数f(x)=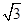 sin(ωx+φ)
(0<φ<π,ω>0)过点
sin(ωx+φ)
(0<φ<π,ω>0)过点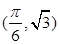 ,函数y=f(x)图象的两相邻对称轴间的距离为
,函数y=f(x)图象的两相邻对称轴间的距离为 .
.
(1) 求f(x)的解析式;
(2) f(x)的图象向右平移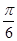 个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
【解析】本试题主要考查了三角函数的图像和性质的运用,第一问中利用函数y=f(x)图象的两相邻对称轴间的距离为 .得
.得 ,
, 所以
所以
第二问中,

 ,
,

 可以得到单调区间。
可以得到单调区间。
解:(Ⅰ)由题意得 ,
, ,…………………1分
,…………………1分
 代入点
代入点 ,得
,得 …………1分
…………1分
 ,
,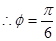 ∴
∴
(Ⅱ) ,
,



 的单调递减区间为
的单调递减区间为 ,
, .
.
查看习题详情和答案>>
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积。
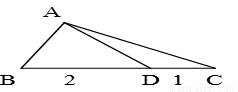
【解析】本试题主要考查了余弦定理的运用。利用由题意得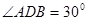 ,
,

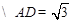 ,
,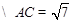 并且
并且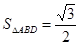 有
有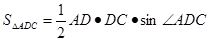 得到结论。
得到结论。
解:(Ⅰ)由题意得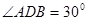 ,
,
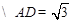 ………1分
………1分 …………1分
…………1分
(Ⅱ)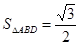 ………………1分
………………1分
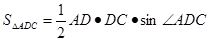
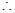
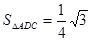
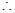

查看习题详情和答案>>
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.[来源:学,科,网Z,X,X,K]
【解析】第一问解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
(11)由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
查看习题详情和答案>>
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
查看习题详情和答案>>