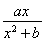摘要：∴直线的斜率为.且与函数的图象的切点坐标为.
网址：http://m.1010jiajiao.com/timu_id_191788[举报]
二次函数y=x2-x-6的图象与坐标轴交于A、B、C三点，圆M为△ABC的外接圆，斜率为2的直线l与圆M相交于不同两点E、F，令EF的中点为N，O为坐标原点，且|ON|=
|EF|．
（Ⅰ）求圆M的方程；
（Ⅱ）求直线l的方程．
查看习题详情和答案>>
| 1 | 2 |
（Ⅰ）求圆M的方程；
（Ⅱ）求直线l的方程．
对于函数f（x）=-2cosx（x∈[0，π]）与函数g(x)=
x2+lnx有下列命题：
①函数f（x）的图象关于x=
对称；②函数g（x）有且只有一个零点；
③函数f（x）和函数g（x）图象上存在平行的切线；
④若函数f（x）在点P处的切线平行于函数g（x）在点Q处的切线，则直线PQ的斜率为
．其中正确的命题是
查看习题详情和答案>>
| 1 |
| 2 |
①函数f（x）的图象关于x=
| π |
| 2 |
③函数f（x）和函数g（x）图象上存在平行的切线；
④若函数f（x）在点P处的切线平行于函数g（x）在点Q处的切线，则直线PQ的斜率为
| 1 |
| 2-π |
②③④
②③④
．（将所有正确命题的序号都填上）定义函数F（x，y）=（1+x）y，x，y∈（0，+∞）．
（1）令函数f（x）=F[1，log2(x3-3x)]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；
（2）令函数g（x）=F[1，log2(x3+ax2+bx+1)]的图象为曲线C2，若存在实数b使得曲线C2在x0（x0∈（1，4））处有斜率为-8的切线，求实数a的取值范围；
（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>
（1）令函数f（x）=F[1，log2(x3-3x)]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；
（2）令函数g（x）=F[1，log2(x3+ax2+bx+1)]的图象为曲线C2，若存在实数b使得曲线C2在x0（x0∈（1，4））处有斜率为-8的切线，求实数a的取值范围；
（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
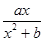，且f(x)的图象在x＝1处与直线y＝2相切．