摘要:(II)0<x<1时.曲线y=f(x)在点P(x0.y0)处的切线方程为:
网址:http://m.1010jiajiao.com/timu_id_191727[举报]
已知函数f(x)的定义域为{x| x ≠ kπ,k ∈ Z},且对于定义域内的任何x、y,有f(x?? - y) = ![]() 成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f (x)在[2a,3a] 上的最小值和最大值.
成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f (x)在[2a,3a] 上的最小值和最大值.
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分

当b<1时, ;
;
当 时,
时, ;
;
当b>2时, ;
............8分
;
............8分
问题等价于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是
查看习题详情和答案>>
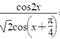 =
=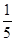 ,0<x<π,则tanx为
,0<x<π,则tanx为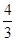 B.-
B.-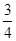 C.2 D.-2
C.2 D.-2