摘要:A.且 B.且 C.且 D.且答案:A
网址:http://m.1010jiajiao.com/timu_id_183702[举报]
小明在《高中全程复习优化训练》中遇到这样一道习题,无法确定答案,请你帮他解决.题目为:下列结论中正确的个数是
①方程(x-1)3(x+5)(x+1)=0的解集为{1,1,1,-5,-1};②实数集{1,a,a2-a}中元素a所满足的条件为a≠0且a≠1且a≠2;③集合A={a,b,c}中的三个元素可构成△ABC三边长,则△ABC一定不是等腰三角形;④方程组 的解集为{(3,1,4)};⑤集合N中的最小元素为1;⑥方程(x-1)3(x+2)(x-5)=0的解集含有3个元素;⑦0∈
的解集为{(3,1,4)};⑤集合N中的最小元素为1;⑥方程(x-1)3(x+2)(x-5)=0的解集含有3个元素;⑦0∈![]() ;⑧满足1+x>x的实数的全体形成集合.
;⑧满足1+x>x的实数的全体形成集合.
[ ]
A.3
B.4
C.5
D.6
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,求线段AE的长.
B.(选修4-2:矩阵与变换)
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
|
|
C.(选修4-4:坐标系与参数方程)
以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,建立极坐标系(两种坐标系中取相同的单位长度),已知点A的直角坐标为(-2,6),点B的极坐标为(4,
| π |
| 2 |
| π |
| 4 |
D.(选修4-5:不等式选讲)
设a,b,c,d都是正数,且x=
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.A.(选修4-1:几何证明选讲)
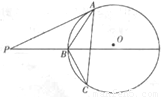
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵
|
C.(选修4-4:坐标系与参数方程)
已知曲线C1:
|
| π |
| 4 |
| 2 |
(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<
| c |
| 4 |
| c |
| 6 |
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4-1:几何证明选讲)
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵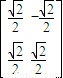 对应的变换作用下得到的曲线C′的方程.
对应的变换作用下得到的曲线C′的方程.
C.(选修4-4:坐标系与参数方程)
已知曲线C1: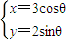 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-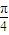 )=
)=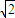 .
.
(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<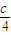 ,|y-b|<
,|y-b|<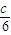 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c.
 查看习题详情和答案>>
查看习题详情和答案>>
A.(选修4-1:几何证明选讲)
过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,∠ABP=∠ABC,C是圆上一点使得BC=5,求线段AB的长.
B.(选修4-2:矩阵与变换)
求曲线C:xy=1在矩阵
 对应的变换作用下得到的曲线C′的方程.
对应的变换作用下得到的曲线C′的方程.C.(选修4-4:坐标系与参数方程)
已知曲线C1:
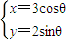 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-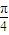 )=
)=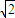 .
.(1)将两曲线方程分别化成普通方程;
(2)求两曲线的交点坐标.
D.(选修4-5:不等式选讲)
已知|x-a|<
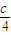 ,|y-b|<
,|y-b|<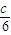 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c. 查看习题详情和答案>>
查看习题详情和答案>>