摘要：记.可知:.
网址：http://m.1010jiajiao.com/timu_id_152507[举报]
已知函数f（x）=aInx-ax，（a∈R）
（1）求f（x）的单调递增区间；（文科可参考公式：(Inx)′=
）
（2）若f′（2）=1，记函数g（x）=x3+x2•[f′(x)+
]，若g（x）在区间（1，3）上总不单调，求实数m的范围．
查看习题详情和答案>>
（1）求f（x）的单调递增区间；（文科可参考公式：(Inx)′=
| 1 |
| x |
（2）若f′（2）=1，记函数g（x）=x3+x2•[f′(x)+
| m |
| 2 |
已知有穷数列A：a1，a2，…，an（n≥2，n∈N）．定义如下操作过程T：从A中任取两项ai，aj，将
的值添在A的最后，然后删除ai，aj，这样得到一系列n-1项的新数列A1 （约定：一个数也视作数列）；对A1的所有可能结果重复操作过程T又得到一系列n-2项的新数列A2，如此经过k次操作后得到的新数列记作Ak．设A：-
，
，
，
，则A3的可能结果是（ ）
| ai+aj |
| 1+aiaj |
| 5 |
| 7 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知可导函数f（x）的导函数为g（x），且满足：①
＞0；②f（2-x）-f（x）=2-2x，记a=f（2）-1，b=f（π）-π+1，c=f（-1）+2，则a，b，c的大小顺序为（ ）
| g(x)-1 |
| x-1 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞c＞a |
| D、b＞a＞c |
已知某海滨浴场的海浪高度y（单位：米）与时间 t（0≤t≤24）（单位：时）的函数关系记作y=f（t），下表是某日各时的浪高数据：
经长期观测，函数y=f（t）可近似地看成是函数y=Acosωt+b．
（1）根据以上数据，求出函数y=Acosωt+b的最小正周期T及函数表达 式（其中A＞0，ω＞0）；
（2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放？ 查看习题详情和答案>>
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
（1）根据以上数据，求出函数y=Acosωt+b的最小正周期T及函数表达 式（其中A＞0，ω＞0）；
（2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放？ 查看习题详情和答案>>
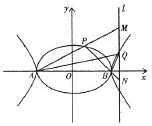已知A，B分别是椭圆C1：