摘要:∴∠QMP=∠FMP=900.且MF=MQ.从而∠FMQ为二面角B-A1P-F的平面角-----10分
网址:http://m.1010jiajiao.com/timu_id_152483[举报]
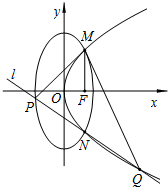 (2013•永州一模)在直角坐标系xoy中,椭圆C1:
(2013•永州一模)在直角坐标系xoy中,椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
(1)求点M的坐标及椭圆C1的方程;
(2)若过点N且斜率为k的直线l交C1于另一点P,交C2于另一点Q,且MP⊥MQ,求k的值.
(2008•临沂二模)已知椭圆C:
+
=1(a>b>0)的离心率为
,F为右焦点,M、N两点在椭圆C上,且
=λ
(λ>0)定点A(-4,0)
(I)求证:当λ=1时,有
⊥
;
(Ⅱ)若λ=1时,有
•
=
,求椭圆C的方程.
(Ⅲ)在(Ⅱ)确定的椭圆C上,当
•
×tan∠MAN的值为6
时,求直线MN的方程.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| MF |
| FN |
(I)求证:当λ=1时,有
| MN |
| AF |
(Ⅱ)若λ=1时,有
| AM |
| AN |
| 106 |
| 3 |
(Ⅲ)在(Ⅱ)确定的椭圆C上,当
| AM |
| AN |
| 3 |
已知抛物线C1:y=x2,F为抛物线的焦点,椭圆C2:
+
=1(0<a<2);
(1)若M是C1与C2在第一象限的交点,且|MF|=
,求实数a的值;
(2)设直线l:y=kx+1与抛物线C1交于A,B两个不同的点,l与椭圆C2交于P,Q两个不同点,AB中点为R,PQ中点为S,若O在以RS为直径的圆上,且k 2>
,求实数a的取值范围.
查看习题详情和答案>>
| x2 |
| 2 |
| y2 |
| a2 |
(1)若M是C1与C2在第一象限的交点,且|MF|=
| 3 |
| 4 |
(2)设直线l:y=kx+1与抛物线C1交于A,B两个不同的点,l与椭圆C2交于P,Q两个不同点,AB中点为R,PQ中点为S,若O在以RS为直径的圆上,且k 2>
| 1 |
| 2 |
 (2012•西区模拟)已知椭圆
(2012•西区模拟)已知椭圆